题目内容
4．设集合M={x|2x+1＞1}，N={x|lnx≤1}，则M∩N等于（ ）| A． | （-∞，e] | B． | （-1，1] | C． | （0，1） | D． | （0，e] |
分析 先分别求出集合M，N，由此能求出M∩N．
解答 解：∵M={x|2x+1＞1}={x|x＞-1}，
N={x|lnx≤1}={x|0＜x≤e}，
∴M∩N=（0，e]．
故选：D．
点评 本题考查交集的求法，是基础题，解题时要认真审题，注意交集定义的合理运用．
练习册系列答案
相关题目
14．在区间[1，6]上随机地取一个数x，则事件“$1≤log_2^{\;}x≤2$”发生的概率为（ ）
| A． | $\frac{4}{5}$ | B． | $\frac{3}{5}$ | C． | $\frac{2}{5}$ | D． | $\frac{1}{5}$ |
15．圆柱被一个平面截去一部分后与一个四棱锥组成的几何体的三视图如图所示，则该几何体的体积为（ ）
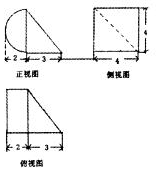
| A． | 4π+8 | B． | 8π+16 | C． | 16π+16 | D． | 16π+48 |
12．若$x∈（{e，{e^2}}），a=lnx，b={（{\frac{1}{2}}）^{lnx}}，c={e^{lnx}}$，则a，b，c的大小关系为（ ）
| A． | c＞b＞a | B． | c＞a＞b | C． | a＞b＞c | D． | b＞c＞a |
19．已知双曲线的渐近线方程为y=±$\frac{3}{4}$x，则此双曲线的（ ）
| A． | 焦距为10 | B． | 实轴长与虚轴长分别为8与6 | ||
| C． | 离心率e只能是$\frac{5}{4}$或$\frac{5}{3}$ | D． | 离心率e不可能是$\frac{5}{4}$或$\frac{5}{3}$ |
随着经济模式的改变，微商和电商已成为当今城乡一种新型的购销平台．已知经销某种商品的电商在任何一个销售季度内，每售出1吨该商品可获利润0.5万元，未售出的商品，每1吨亏损0.3万元．根据往年的销售经验，得到一个销售季度内市场需求量的频率分布直方图如右图所示．已知电商为下一个销售季度筹备了130吨该商品．现以x（单位：吨，100≤x≤150）表示下一个销售季度的市场需求量，T（单位：万元）表示该电商下一个销售季度内经销该商品获得的利润．
16．
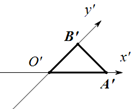如图一个水平放置的三角形的斜二测直观图是等腰直角三角形A′B′O′，若O′B′=B′A′=1，那么原△ABO的面积是（ ）
如图一个水平放置的三角形的斜二测直观图是等腰直角三角形A′B′O′，若O′B′=B′A′=1，那么原△ABO的面积是（ ）| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\sqrt{2}$ | D． | 2$\sqrt{2}$ |
13．下列结论正确的是（ ）
| A． | 事件A的概率P（A）必有0＜P（A）＜1 | |
| B． | 事件A的概率P（A）=0.999，则事件A是必然事件 | |
| C． | 用某种药物对患有胃溃疡的500名病人治疗，结果有380人有明显的疗效，现有胃溃疡的病人服用此药，则估计其有明显的疗效的可能性为76% | |
| D． | 某奖券中奖率为50%，则某人购买此券10张，一定有5张中奖 |