题目内容
7.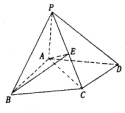 在四棱锥P-ABCD中,△ABC为正三角形,AB⊥AD,AC⊥CD,PA⊥平面ABCD,PC与平面ABCD所成角为45°
在四棱锥P-ABCD中,△ABC为正三角形,AB⊥AD,AC⊥CD,PA⊥平面ABCD,PC与平面ABCD所成角为45°(1)若E为PC的中点,求证:PD⊥平面ABE;
(2)若CD=$\sqrt{3}$,求点B到平面PCD的距离.
分析 (1)利用线面垂直的判定与性质定理可得CD⊥平面PAC,CD⊥AE.利用等腰三角形的性质与线面垂直的判定定理可得:AE⊥平面PCD,可得AE⊥PD.利用面面垂直的性质定理与线面垂直的判定定理可得AB⊥PD,进而证明结论.
(2)设点B的平面PCD的距离为d,利用VB-PCD=VP-BCD即可得出.
解答 (1)证明:∵PA⊥平面ABCD,CD?平面ABCD,∴PA⊥CD.
∵AC⊥CD,PA∩AC=A,∴CD⊥平面PAC,而AE?平面PAC,∴CD⊥AE.
∵PC与平面ABCD所成角为45°
∴AC=PA,
∵E是PC的中点,∴AE⊥PC,又PC∩CD=C,∴AE⊥平面PCD,
而PD?平面PCD,∴AE⊥PD.
∵PA⊥底面ABCD,∴平面PAD⊥平面ABCD,又AB⊥AD,
由面面垂直的性质定理可得BA⊥平面PAD,AB⊥PD,
又AB∩AE=A,∴PD⊥平面ABE.
(2)解:CD=$\sqrt{3}$,可得AC=3,
∵PA⊥平面ABCD,∴PA⊥AC,∴PC=3$\sqrt{2}$,
由(1)的证明知,CD⊥平面PAC,∴CD⊥PC,
∵AB⊥AD,△ABC为正三角形,∴∠CAD=30°,
∵AC⊥CD,∴CD=ACtan30°=$\sqrt{3}$.
设点B的平面PCD的距离为d,则VB-PCD=$\frac{1}{3}$×$\frac{1}{2}$×3$\sqrt{2}$×$\sqrt{3}$×d=$\frac{\sqrt{6}}{2}$d.
在△BCD中,∠BCD=150°,∴S△BCD=$\frac{1}{2}$×3×$\sqrt{3}$sin150°=$\frac{3\sqrt{3}}{4}$.
∴VP-BCD=$\frac{1}{3}$×$\frac{3\sqrt{3}}{4}$×3=$\frac{3\sqrt{3}}{4}$,
∵VB-PCD=VP-BCD,∴$\frac{\sqrt{6}}{2}$d=$\frac{3\sqrt{3}}{4}$,解得d=$\frac{3\sqrt{2}}{4}$,
即点B到平面PCD的距离为$\frac{3\sqrt{2}}{4}$.
点评 本题考查了空间位置关系、线面面面垂直的判定与性质定理、三棱锥的体积计算公式,考查了推理能力与计算能力,属于中档题.

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
| A. | 4π+8 | B. | 8π+16 | C. | 16π+16 | D. | 16π+48 |
| A. | c>b>a | B. | c>a>b | C. | a>b>c | D. | b>c>a |
| A. | 焦距为10 | B. | 实轴长与虚轴长分别为8与6 | ||
| C. | 离心率e只能是$\frac{5}{4}$或$\frac{5}{3}$ | D. | 离心率e不可能是$\frac{5}{4}$或$\frac{5}{3}$ |
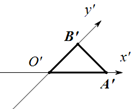 如图一个水平放置的三角形的斜二测直观图是等腰直角三角形A′B′O′,若O′B′=B′A′=1,那么原△ABO的面积是( )
如图一个水平放置的三角形的斜二测直观图是等腰直角三角形A′B′O′,若O′B′=B′A′=1,那么原△ABO的面积是( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既充分也不必要条件 |