题目内容
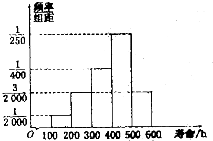对某种电子元件的使用寿命进行跟踪调查，所得样本的频率分布直方图如图所示，由图可知，这一批电子元件中使用寿命在100～300h的电子元件的数量与使用寿命在300～600h的电子元件的数量的比是考点：频率分布直方图
专题：概率与统计
分析：由已知中的频率分布直方图，我们易求出寿命在100～300小时的电子元件的数量与寿命在300～600小时的电子元件的频率，进而总体分布与样本分布之间的关系，即可得到寿命在100～300小时的电子元件的数量与寿命在300～600小时的电子元件的数量的比．
解答：
解：由于已知的频率分布直方图中组距为100，
寿命在100～300小时的电子元件对应的矩形的高分别为：
，
则寿命在100～300小时的电子元件的频率为：100•（
+
）=0.2
寿命在300～600小时的电子元件对应的矩形的高分别为：
，
，
则寿命在300～600小时子元件的频率为：100•（
+
+
）=0.8
则寿命在100～300小时的电子元件的数量与寿命在300～600小时的电子元件的数量的比大约是0.2：0.8=．
故答案为：
．
寿命在100～300小时的电子元件对应的矩形的高分别为：
| 1 |
| 2000 |
| 3 |
| 2000 |
则寿命在100～300小时的电子元件的频率为：100•（
| 1 |
| 2000 |
| 1 |
| 2000 |
寿命在300～600小时的电子元件对应的矩形的高分别为：
| 1 |
| 400 |
| 1 |
| 250 |
| 1 |
| 2000 |
则寿命在300～600小时子元件的频率为：100•（
| 1 |
| 400 |
| 1 |
| 250 |
| 3 |
| 2000 |
则寿命在100～300小时的电子元件的数量与寿命在300～600小时的电子元件的数量的比大约是0.2：0.8=．
故答案为：
| 1 |
| 4 |
点评：本题考查的知识点是用样本的频率分布估计总体分布，其中由已知的频率分布直方图，其中根据频率分布直方图，我们可以根据频率=组距×矩形的高，得到各段数据的频率是解答本题的关键．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
双曲线
-
=1的离心率为2，则该双曲线的渐近线方程为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| A、x±2y=0 | ||
| B、2x±y=0 | ||
C、
| ||
D、x±
|
已知全集U=R，A={x|x2-x-2＜0}，B={x|x≥0}，则A∪B=（ ）
| A、{x|0≤x＜2} |
| B、{x|x≥0} |
| C、{x|x≤-1} |
| D、{x|x＞-1} |