题目内容
从0至4五个自然数中任意取出不同三个，分别作为关于x的方程ax2+bx+c=0的系数，则所得方程有实数解的取法有 ．
考点：计数原理的应用
专题：计算题
分析：分2种情况讨论：①、若ac=0，分析易得方程ax2+bx+c=0必有解，由排列数公式易得其情况数目，②、若ac≠0，由二次函数的性质可得方程ax2+bx+c=0有解?b2-4ac≥0，列举可能的情况可得其情况数目，由分类计数原理，计算即可得答案．
解答：
解：根据题意，分2种情况讨论：
①、若ac=0即a=0或c=0，
若a=0，则方程ax2+bx+c=0为一次方程，必有解，此时有A42=12种情况，
若c=0，则有b2-4ac=b2＞0，方程ax2+bx+c=0必有解，此时有A42=12种情况，
此时有C21A42=24种情况，
②、若ac≠0，则方程ax2+bx+c=0有解?b2-4ac≥0，
若b=4，则ac的情况有1、2，1、3，2、1，3、1，共4种情况，
若b=3，则ac的情况有1、2，2、1，共2种情况，
则所得方程有实数解的取法有30种；
故答案为30．
①、若ac=0即a=0或c=0，
若a=0，则方程ax2+bx+c=0为一次方程，必有解，此时有A42=12种情况，
若c=0，则有b2-4ac=b2＞0，方程ax2+bx+c=0必有解，此时有A42=12种情况，
此时有C21A42=24种情况，
②、若ac≠0，则方程ax2+bx+c=0有解?b2-4ac≥0，
若b=4，则ac的情况有1、2，1、3，2、1，3、1，共4种情况，
若b=3，则ac的情况有1、2，2、1，共2种情况，
则所得方程有实数解的取法有30种；
故答案为30．
点评：本题考查分类计数原理的运用，注意不要遗漏a=0时，方程ax2+bx+c=0是一次方程的情况．
练习册系列答案
相关题目
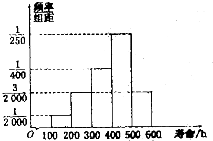对某种电子元件的使用寿命进行跟踪调查，所得样本的频率分布直方图如图所示，由图可知，这一批电子元件中使用寿命在100～300h的电子元件的数量与使用寿命在300～600h的电子元件的数量的比是已知i是虚数单位，m∈R，且
是纯虚数，则（
）2008等于（ ）
| 2-mi |
| 1+i |
| 2-mi |
| 2+mi |
| A、1 | B、-1 | C、i | D、-i |
已知两点A（-1，5），B（3，9），则线段AB的中点坐标为（ ）
| A、（1，7） |
| B、（2，2） |
| C、（-2，-2） |
| D、（2，14） |