题目内容

在平行四边形ABCD中，AB=2，AD=1，∠A=60°，点M在AB上，且AM=
1
3
AB，则
.
DM
•
.
DB
等于
 
．
考点：平面向量数量积的运算
专题：平面向量及应用
分析：根据向量的减法运算用
AB
、
AD
表示出
DM
和
DB
，由数量积的运算律化简
DM
•
DB
，根据条件求值即可．
解答： 解：由题意画出图形如右图：
∵点M在AB上，且AM=
1
3
AB，∴
AM
=
1
3
AB
，
∵
DM
=
AM
-
AD
=
1
3
AB
-
AD
，
DB
=
AB
-
AD

且AB=2，AD=1，∠A=60°，
∴
DM
•
DB
=（
1
3
AB
-
AD
）•（
AB
-
AD
）
=
1
3
AB
2-
4
3
AB
•
AD
+
AD
2
=
1
3
×4-
4
3
×2×1×
1
2
+1
=1，
故答案为1．
点评：本题考查了向量的减法运算和数量积的定义、运算律的应用，此题的关键是用
AB
、
AD
表示出
DM
和
DB
．
练习册系列答案
相关题目
已知函数f（x）=ax3+|x-a|（a∈R）．
（1）是否存在实数a，使得函数f（x）在（-∞，0]上单调递减，在[0，+∞）上单调递增？请说明理由；
（2）若0＜a＜1，求函数f（x）在[-1，1]上的最大值；
（3）求证：对任意的实数a，存在x0，恒有f（x0）≠0，并求出符合该特征的x0的取值范围．
某品牌生产企业的三个车间在三月份共生产了4800件产品，企业质检部门要对这批产品进行质检，他们用分层抽样的方法，从一，二，三车间分别抽取的产品数为a，b，c，若a，b，c构成等差数列，则第二车间生产的产品数为
 
．
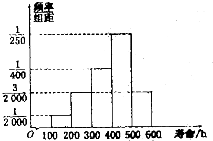对某种电子元件的使用寿命进行跟踪调查，所得样本的频率分布直方图如图所示，由图可知，这一批电子元件中使用寿命在100～300h的电子元件的数量与使用寿命在300～600h的电子元件的数量的比是
 
．
在极坐标系中，设P是直线l：ρ（cosθ-2sinθ）=6上任一点，Q是圆C：
x=1+
2
cosφ
y=
2
sinφ
（φ为参数）上任一点，则|PQ|的最小值
 
．
在平面直角坐标系xOy中，已知圆O：x2+y2=4，直线l：12x-5y+c=0（其中c为常数），下列有关直线l与圆O的命题：
①当c=0时，圆O上有四个不同点到直线l的距离为1；
②若圆O上有四个不同点到直线l的距离为1，则-13＜c＜13；
③若圆O上恰有三个不同点到直线l的距离为1，则c=13；
④若圆O上恰有两个不同点到直线l的距离为1，则13＜c＜39；
⑤当c=±39时，圆O上只有一个点到直线l的距离为1．
其中正确命题的有
 
（填上你认为正确的所有命题的序号）
设复数z=（1-i）2（i为虚数单位），则
.
z
的虚部（　　）
A、2iB、-2iC、2D、-2
已知：复数z=
1
2
+
3
2
i，它的共轭复数为
.
z
，则
.
z
2=（　　）
A、-
1
2
+
3
2
i
B、
1
2
-
3
2
i
C、-
1
2
-
3
2
i
D、
1
2
+
3
2
i
设i是虚数单位，复数z=
1-ai
1+i
（a∈R）为纯虚数，则复数z的虚部为（　　）
A、-iB、-2iC、-1D、-2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网