题目内容
已知函数f（x）=4cosωx•sin（ωx+
）（ω＞0）的最小正周期为π．
（1）讨论f（x）在区间[0，
]上的单调性；
（2）若在△ABC满足f（A+
）=
-1（0＜A＜
），面积S=5
，边长b=5，求sinBsinC的值．
| π |
| 4 |
（1）讨论f（x）在区间[0，
| π |
| 2 |
（2）若在△ABC满足f（A+
| π |
| 8 |
| 2 |
| π |
| 2 |
| 3 |
考点：余弦定理,正弦函数的单调性,正弦定理,正弦定理的应用
专题：三角函数的图像与性质,解三角形
分析：（1）通过两角和与差的三角函数化简函数的表达式为 一个角的一个三角函数的形式，讨论f（x）在区间[0，
]上的单调性；
（2）通过f（A+
）=
-1（0＜A＜
），求出A，利用面积S=5
，求出b，c，利用余弦定理求出a，然后利用正弦定理求sinBsinC的值．
| π |
| 2 |
（2）通过f（A+
| π |
| 8 |
| 2 |
| π |
| 2 |
| 3 |
解答：
解：（1）函数f（x）=4cosωx•sin（ωx+
）
=4cosωx•（
sinωx+
cosωx）
=
sin2ωx+2
cos2ωx
=
sin2ωx+
（1+cos2ωx）
=2sin(2ωx+
)+
，
∵最小正周期为π，且ω＞0
∴ω=1，则f(x)=2sin(2x+
)+
若0≤x≤
，则
≤2x+
≤
，
当
≤2x+
≤
，即y=f（x）在[0，
]是单调递增．
当
≤2x+
≤
，即y=f（x）在[
，
]是单调递减．
综上可知，f（x）在区间[0，
]是单调递增，在区间[
，
]是单调递减．
（2）由条件f（A+
）=
-1
得
-1=2sin(2A+
+
)+
，
即cos2A=-
，0＜A＜
，
∴A=
，由面积S=5
，得bc=20，又b=5知c=4
由余弦定理a2=b2+c2-2bccosA，
得a=
，
由正弦定理2R=
=
=2
，得sinCsinB=
=
．
| π |
| 4 |
=4cosωx•（
| ||
| 2 |
| ||
| 2 |
=
| 2 |
| 2 |
=
| 2 |
| 2 |
=2sin(2ωx+
| π |
| 4 |
| 2 |
∵最小正周期为π，且ω＞0
∴ω=1，则f(x)=2sin(2x+
| π |
| 4 |
| 2 |
若0≤x≤
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 5π |
| 4 |
当
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| π |
| 8 |
当
| π |
| 2 |
| π |
| 4 |
| 5π |
| 4 |
| π |
| 8 |
| π |
| 2 |
综上可知，f（x）在区间[0，
| π |
| 8 |
| π |
| 8 |
| π |
| 2 |
（2）由条件f（A+
| π |
| 8 |
| 2 |
得
| 2 |
| π |
| 4 |
| π |
| 4 |
| 2 |
即cos2A=-
| 1 |
| 2 |
| π |
| 2 |
∴A=
| π |
| 3 |
| 3 |
由余弦定理a2=b2+c2-2bccosA，
得a=
| 21 |
由正弦定理2R=
| a |
| sinA |
| ||||
|
| 7 |
| bc |
| 4R2 |
| 5 |
| 7 |
点评：本题考查解三角形，两角和与差的三角函数以及函数的单调性的讨论，正弦定理以及余弦定理的应用，是综合性比较强的题目．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
设函数f（x）=
，g（x）=
，则函数f（x）•g（x）的定义域是（ ）
| 3 | 3x-2 |
| 1 | ||
|
A、[
| ||||
B、（
| ||||
C、[
| ||||
D、（
|
某工厂随机抽取处12件A型产品和18件B型产品，将这30件产品的尺寸编成如图所示的茎叶图（单位：cm），若尺寸在175cm以上（包括175cm）的产品定义为“标准件”，尺寸在175cm以下（不包括175cm）的产品定义为“非标准件”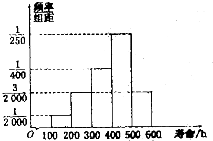
对某种电子元件的使用寿命进行跟踪调查，所得样本的频率分布直方图如图所示，由图可知，这一批电子元件中使用寿命在100～300h的电子元件的数量与使用寿命在300～600h的电子元件的数量的比是