题目内容
已知函数f（x）=
则f（2014.5）= ；若关于x的方程f（x）=x+a有且只有两个不相等的实数根，则实数a的取值范围是 ．
|
考点：函数的图象,函数的值,函数的零点
专题：函数的性质及应用
分析：利用函数在x＞0时，具有周期性，化简f（2014.5）为f（-0.5）然后求解即可．第二问：画出函数的图象即可求解a的范围．
解答：
解：第一问：函数f（x）=
，当x＞0时函数值具有周期性变化，周期是1，
则f（2014.5）=f（2004+0.5）=f（0.5）=f（-0.5）=40.5-1=2-1=1．
故答案为：1．
第二问，在同一直角坐标系内画出函数y=f（x）和y=x+a的图象如图可知a＜1．
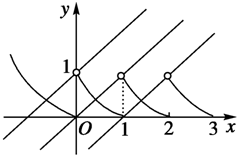
故答案为：（-∞，1）．
|
则f（2014.5）=f（2004+0.5）=f（0.5）=f（-0.5）=40.5-1=2-1=1．
故答案为：1．
第二问，在同一直角坐标系内画出函数y=f（x）和y=x+a的图象如图可知a＜1．
故答案为：（-∞，1）．
点评：本题考查函数的值的求法，函数的图象的应用，考查数形结合以及函数的基本性质的应用．
练习册系列答案
相关题目
某工厂随机抽取处12件A型产品和18件B型产品，将这30件产品的尺寸编成如图所示的茎叶图（单位：cm），若尺寸在175cm以上（包括175cm）的产品定义为“标准件”，尺寸在175cm以下（不包括175cm）的产品定义为“非标准件”
对某种电子元件的使用寿命进行跟踪调查，所得样本的频率分布直方图如图所示，由图可知，这一批电子元件中使用寿命在100～300h的电子元件的数量与使用寿命在300～600h的电子元件的数量的比是设复数z=（1-i）2（i为虚数单位），则
的虚部（ ）
. |
| z |
| A、2i | B、-2i | C、2 | D、-2 |
不等式|3-2x|＜1的解集为（ ）
| A、（-2，2） |
| B、（2，3） |
| C、（1，2） |
| D、（3，4） |