题目内容

若x1，x2是方程πsin
x
4
=0的两个零点，且x1＜x2，则x2-x1的最小值是
 
．
考点：正弦函数的图象
专题：三角函数的图像与性质
分析：求出函数的周期，利用函数零点的意义，得到结论．
解答： 解：函数f（x）=πsin
x
4
的周期为8π，
若x1，x2是方程πsin
x
4
=0的两个零点，
则x2-x1的最小值是半个周期，即4π．
故答案为：4π．
点评：本题主要考查正弦函数的图象和性质，利用条件求出函数的周期是解决本题的关键，任意两个零点之间的距离和周期出存在一定的关系．
练习册系列答案
相关题目
有编号为1，2，3，…，n的n名学生，入坐编号为1，2，3，…，n的n个座位，规定每个学生可随机坐一个座位，记学生所坐的座位编号与该生的编号不同的学生数为X，若当X=2时，共有6种坐法．
（Ⅰ）求n的值；
（Ⅱ）求2号学生未坐2号座位且4号学生入坐4号座位的概率；
（Ⅲ）求随机变量X的数学期望．
已知f（x）定义在R上的奇函数，且它的图象关于直线x=1对称，若函数f（x）=
x
，（0＜x≤1），则f（-5.5）=
 
．
方程
x|x|
16
+
y|y|
9
=λ（λ＜0）的曲线即为函数y=f（x）的图象，对于函数y=f（x），下列命题中正确的是
 
．（请写出所有正确命题的序号）
①函数y=f（x）在R上是单调递减函数；
②函数y=f（x）的值域是R；
③函数y=f（x）的图象不经过第一象限；
④函数y=f（x）的图象关于直线y=x对称；
⑤函数F（x）=4f（x）+3x至少存在一个零点．
某品牌生产企业的三个车间在三月份共生产了4800件产品，企业质检部门要对这批产品进行质检，他们用分层抽样的方法，从一，二，三车间分别抽取的产品数为a，b，c，若a，b，c构成等差数列，则第二车间生产的产品数为
 
．
已知实数x，y满足
2x-y≤0
x-3y+5≥0
y≥1
，则z=x+y-2的取值范围是
 
．
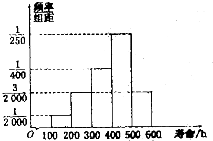对某种电子元件的使用寿命进行跟踪调查，所得样本的频率分布直方图如图所示，由图可知，这一批电子元件中使用寿命在100～300h的电子元件的数量与使用寿命在300～600h的电子元件的数量的比是
 
．
在平面直角坐标系xOy中，已知圆O：x2+y2=4，直线l：12x-5y+c=0（其中c为常数），下列有关直线l与圆O的命题：
①当c=0时，圆O上有四个不同点到直线l的距离为1；
②若圆O上有四个不同点到直线l的距离为1，则-13＜c＜13；
③若圆O上恰有三个不同点到直线l的距离为1，则c=13；
④若圆O上恰有两个不同点到直线l的距离为1，则13＜c＜39；
⑤当c=±39时，圆O上只有一个点到直线l的距离为1．
其中正确命题的有
 
（填上你认为正确的所有命题的序号）
已知复数z1、z2在复平面上对应的点分别为A（1，2）、B（-1，3），则
z2
z1
的虚部为（　　）
A、1B、iC、-1D、-i

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网