题目内容

设t∈R，[t]表示不超过t的最大整数．则在平面直角坐标系xOy中，满足[x]2+[y]2=13的点P（x，y）所围成的图形的面积为
 
．
考点：进行简单的演绎推理
专题：推理和证明
分析：根据方程可得对于x，y≥0时，求出x，y的整数解，可得|[x]|可能取的数值为2，则可以确定x的范围，进而得到对应的y的范围，求出面积即可．
解答： 解：由题意可得：方程：[x]2+[y]2=13，
当x，y≥0时，[x]，[y]的整数解为（2，3），所以此时x可能取的数值为：2．
所以当|[x]|=2时，2≤x＜3，或者-2≤x＜-1，|[y]|=3，3≤y＜4，或者-3≤y＜-2，围成的区域是8个单位正方形，
所以满足[x]2+[y]2=13的点P（x，y）所成的图形面积为8．
故答案为：8．
点评：本题考查探究性问题，是创新题，考查学生分析问题，解决问题的能力，属于中档题．
练习册系列答案
相关题目
春节期间，某商场进行促销活动，方案是：顾客每买满200元可按以下方式摸球兑奖：箱内装有标着数字20，40，60，80，1 00的小球各两个，顾客从箱子里任取三个小球，按三个小球中最大数字等额返还现金（单位：元），每个小球被取到的可能性相等．
（Ⅰ）若有三位顾客各买了268元的商品，求至少有二个返奖不少于80元的概率；
（Ⅱ）在（Ⅰ）的条件下，设返奖不少于80元的人数为ξ，求ξ的数学期望．
已知函数f（x）=ax3+|x-a|（a∈R）．
（1）是否存在实数a，使得函数f（x）在（-∞，0]上单调递减，在[0，+∞）上单调递增？请说明理由；
（2）若0＜a＜1，求函数f（x）在[-1，1]上的最大值；
（3）求证：对任意的实数a，存在x0，恒有f（x0）≠0，并求出符合该特征的x0的取值范围．
已知f（x）定义在R上的奇函数，且它的图象关于直线x=1对称，若函数f（x）=
x
，（0＜x≤1），则f（-5.5）=
 
．
已知数列{an}的前n项和为Sn，并满足：an=2an+1-an+2，a7=4-a3，则S9=
 
．
方程
x|x|
16
+
y|y|
9
=λ（λ＜0）的曲线即为函数y=f（x）的图象，对于函数y=f（x），下列命题中正确的是
 
．（请写出所有正确命题的序号）
①函数y=f（x）在R上是单调递减函数；
②函数y=f（x）的值域是R；
③函数y=f（x）的图象不经过第一象限；
④函数y=f（x）的图象关于直线y=x对称；
⑤函数F（x）=4f（x）+3x至少存在一个零点．
某品牌生产企业的三个车间在三月份共生产了4800件产品，企业质检部门要对这批产品进行质检，他们用分层抽样的方法，从一，二，三车间分别抽取的产品数为a，b，c，若a，b，c构成等差数列，则第二车间生产的产品数为
 
．
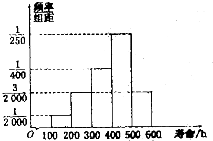对某种电子元件的使用寿命进行跟踪调查，所得样本的频率分布直方图如图所示，由图可知，这一批电子元件中使用寿命在100～300h的电子元件的数量与使用寿命在300～600h的电子元件的数量的比是
 
．
已知：复数z=
1
2
+
3
2
i，它的共轭复数为
.
z
，则
.
z
2=（　　）
A、-
1
2
+
3
2
i
B、
1
2
-
3
2
i
C、-
1
2
-
3
2
i
D、
1
2
+
3
2
i

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网