题目内容
已知全集U=R,A={x|x2-x-2<0},B={x|x≥0},则A∪B=( )
| A、{x|0≤x<2} |
| B、{x|x≥0} |
| C、{x|x≤-1} |
| D、{x|x>-1} |
考点:并集及其运算
专题:集合
分析:求出A中不等式的解集确定出A,找出A与B的并集即可.
解答:
解:由A中不等式变形得:(x-2)(x+1)<0,
解得:-1<x<2,即A={x|-1<x<2},
∵B={x|x≥0},
∴A∪B={x|x>-1}.
故选:D.
解得:-1<x<2,即A={x|-1<x<2},
∵B={x|x≥0},
∴A∪B={x|x>-1}.
故选:D.
点评:此题考查了并集及其运算,熟练掌握并集的定义是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知:复数z=
+
i,它的共轭复数为
,则
2=( )
| 1 |
| 2 |
| ||
| 2 |
. |
| z |
. |
| z |
A、-
| ||||||
B、
| ||||||
C、-
| ||||||
D、
|
已知复数z1、z2在复平面上对应的点分别为A(1,2)、B(-1,3),则
的虚部为( )
| z2 |
| z1 |
| A、1 | B、i | C、-1 | D、-i |
不等式|3-2x|<1的解集为( )
| A、(-2,2) |
| B、(2,3) |
| C、(1,2) |
| D、(3,4) |
已知两点A(-1,5),B(3,9),则线段AB的中点坐标为( )
| A、(1,7) |
| B、(2,2) |
| C、(-2,-2) |
| D、(2,14) |
设i是虚数单位,复数z=
(a∈R)为纯虚数,则复数z的虚部为( )
| 1-ai |
| 1+i |
| A、-i | B、-2i | C、-1 | D、-2 |
双曲线2y2-x2=4的虚轴长是( )
A、
| ||
| B、2 | ||
C、2
| ||
| D、4 |
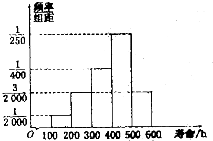 对某种电子元件的使用寿命进行跟踪调查,所得样本的频率分布直方图如图所示,由图可知,这一批电子元件中使用寿命在100~300h的电子元件的数量与使用寿命在300~600h的电子元件的数量的比是
对某种电子元件的使用寿命进行跟踪调查,所得样本的频率分布直方图如图所示,由图可知,这一批电子元件中使用寿命在100~300h的电子元件的数量与使用寿命在300~600h的电子元件的数量的比是