题目内容
14.设{an}是公差不为0的等差数列,满足a42+a52=a62+a72,则{an}的前10项和S10=( )| A. | -10 | B. | -5 | C. | 0 | D. | 5 |
分析 a42+a52=a62+a72,化简可得:$({a_6}^2-{a_4}^2)+({a_7}^2-{a_5}^2)=0$,可得a5+a6=0,再利用等差数列通项公式求和公式及其性质即可得出.
解答 解:a42+a52=a62+a72,化简可得:$({a_6}^2-{a_4}^2)+({a_7}^2-{a_5}^2)=0$,
即2d(a6+a4)+2d(a7+a5)=0,d≠0.
∴a6+a4+a7+a5=0,
∵a5+a6=a4+a7,
∴a5+a6=0,
∴S10=$\frac{10({a}_{1}+{a}_{10})}{2}$=5(a5+a6)=0,
故选:C.
点评 本题考查了等差数列通项公式求和公式及其性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
2.《九章算术》“勾股”章有一题:“今有二人同立.甲行率七,乙行率三,乙东行,甲南行十步而斜东北与乙会,问甲乙各行几何?”大意是说:“已知甲、乙二人同时从同一地点出发,甲的速度为7,乙的速度为3,乙一直向东走,甲先向南走10步,后又斜向北偏东方向走了一段后与乙相遇.甲、乙各走了多少步?”请问乙走的步数是( )
| A. | $\frac{9}{2}$ | B. | $\frac{15}{2}$ | C. | $\frac{21}{2}$ | D. | $\frac{49}{2}$ |
9.执行所给的程序框图,则输出的值是( )


| A. | $\frac{1}{55}$ | B. | $\frac{1}{58}$ | C. | $\frac{1}{61}$ | D. | $\frac{1}{64}$ |
3.等腰直角三角形ABC中,∠C=90°,AC=BC=2,点P是△ABC斜边上任意一点,则线段CP的长度不大于$\sqrt{3}$的概率是( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{2}}}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{6}}}{4}$ |
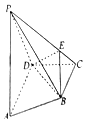 如图,四棱锥P-ABCD中,AD∥BC,AD⊥DC,AD=2BC=2,在侧面PAD中,PA=PD,E为侧棱PC上不同于端点的任意一点且PA⊥DE.
如图,四棱锥P-ABCD中,AD∥BC,AD⊥DC,AD=2BC=2,在侧面PAD中,PA=PD,E为侧棱PC上不同于端点的任意一点且PA⊥DE.