题目内容
5.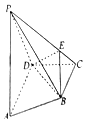 如图,四棱锥P-ABCD中,AD∥BC,AD⊥DC,AD=2BC=2,在侧面PAD中,PA=PD,E为侧棱PC上不同于端点的任意一点且PA⊥DE.
如图,四棱锥P-ABCD中,AD∥BC,AD⊥DC,AD=2BC=2,在侧面PAD中,PA=PD,E为侧棱PC上不同于端点的任意一点且PA⊥DE.(1)证明:平面PAD⊥平面ABCD;
(2)若PA∥平面BDE,求$\frac{CE}{PE}$的值.
分析 (1)推导出PA⊥平面PCD,从而PA⊥CD,再由AD⊥DC,推导出CD⊥平面PAD,由此能证明平面PAD⊥平面ABCD.
(2)连结AC,交BD于O,连结OE,推导出PA∥OE,从而$\frac{CE}{PE}=\frac{CO}{AO}$,由此能求出结果.
解答 证明:(1)∵E是侧棱PC上不同于端点的任意一点,且PA⊥DE,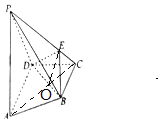
∴PA⊥平面PCD,
∵CD?平面PCD,∴PA⊥CD,
∵AD⊥DC,PA∩AD=A,PA,AD?平面PAD,
∴CD⊥平面PAD,
∵CD?平面ABCD,∴平面PAD⊥平面ABCD.
解:(2)连结AC,交BD于O,连结OE,
∴平面PAD∩平面BDE于O,
∵PA∥平面BDE,PA?平面PAC,
∴PA∥OE,∴$\frac{CE}{PE}=\frac{CO}{AO}$,
∵AD∥BC,AD=2BC,
∴$\frac{CO}{AO}=\frac{CB}{AD}=\frac{1}{2}$,
∴$\frac{CE}{PE}$=$\frac{1}{2}$.
点评 本题考查面面垂直的证明,考查两线段比值的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想、数形结合思想,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.函数f(x)是定义在R上的偶函数,其导函数为f′(x),当x<0时,3f(x)+xf′(x)<0恒成立,则下列结论正确的是( )
| A. | f(1)<2016f($\root{3}{2016}$)<2017f($\root{3}{2017}$) | B. | 2017f($\root{3}{2017}$)<f(1)<2016f($\root{3}{2016}$) | ||
| C. | 2016f($\root{3}{2016}$)<f(1)<2017f($\root{3}{2017}$) | D. | 2017f($\root{3}{2017}$)<2016f($\root{3}{2016}$)<f(1) |
18.在学校体育节中,某班全体40名同学参加跳绳、踢毽子两项比赛的人数统计如下:
(1)从该班随机选1名同学,求该同学至少参加上述一项活动的概率;
(2)已知既参加跳绳又参加踢毽的9名同学中,有男生5名,女生4名,现从这5名男生,4名女生中各随机挑选1人,求男同学甲未被选中且女同学乙被选中的概率.
| 参加跳绳的同学 | 未参加跳绳的同学 | |
| 参加踢毽的同学 | 9 | 4 |
| 未参加踢毽的同学 | 7 | 20 |
(2)已知既参加跳绳又参加踢毽的9名同学中,有男生5名,女生4名,现从这5名男生,4名女生中各随机挑选1人,求男同学甲未被选中且女同学乙被选中的概率.
13.已知平面向量$\overrightarrow a,\overrightarrow b,\overrightarrow c$满足$|{\overrightarrow a}|=4$,$|{\overrightarrow b}|=3$,$|{\overrightarrow c}|=2$,$\overrightarrow b•\overrightarrow c=3$,则${(\overrightarrow a-\overrightarrow b)^2}{(\overrightarrow a-\overrightarrow c)^2}-{[(\overrightarrow a-\overrightarrow b)•(\overrightarrow a-\overrightarrow c)]^2}$最大值为( )
| A. | $4\sqrt{3}+3\sqrt{7}$ | B. | $4\sqrt{7}+3\sqrt{3}$ | C. | ${(4\sqrt{3}+3\sqrt{7})^2}$ | D. | ${(4\sqrt{7}+3\sqrt{3})^2}$ |
14.设{an}是公差不为0的等差数列,满足a42+a52=a62+a72,则{an}的前10项和S10=( )
| A. | -10 | B. | -5 | C. | 0 | D. | 5 |
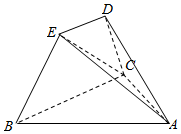 如图所示,四棱锥A-BCDE,已知平面BCDE⊥平面ABC,BE⊥EC,DE∥BC,BC=2DE=6,AB=4$\sqrt{3}$,∠ABC=30°.
如图所示,四棱锥A-BCDE,已知平面BCDE⊥平面ABC,BE⊥EC,DE∥BC,BC=2DE=6,AB=4$\sqrt{3}$,∠ABC=30°.