题目内容
4.在平面直角坐标系中,已知点A,B分别为x轴、y轴上的点,且|AB|=1,若点P(1,$\frac{4}{3}})$),则$|{\overrightarrow{AP}+\overrightarrow{BP}+\overrightarrow{OP}}$|的取值范围是( )| A. | [5,6] | B. | [5,7] | C. | [4,6] | D. | [6,9] |
分析 设A(x,0),B(0,y)求出则$|{\overrightarrow{AP}+\overrightarrow{BP}+\overrightarrow{OP}}$|的模长表达式,根据距离公式的几何意义求出最值.
解答 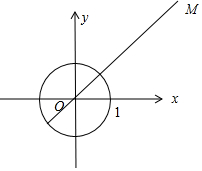 解:设A(x,0),B(0,y),则$\overrightarrow{AP}$=(1-x,$\frac{4}{3}$),$\overrightarrow{BP}$=(1,$\frac{4}{3}$-y),$\overrightarrow{OP}$=(1,$\frac{4}{3}$),
解:设A(x,0),B(0,y),则$\overrightarrow{AP}$=(1-x,$\frac{4}{3}$),$\overrightarrow{BP}$=(1,$\frac{4}{3}$-y),$\overrightarrow{OP}$=(1,$\frac{4}{3}$),
∴$\overrightarrow{AP}+\overrightarrow{BP}+\overrightarrow{OP}$=(3-x,4-y),
∴|$\overrightarrow{AP}+\overrightarrow{BP}+\overrightarrow{OP}$|=$\sqrt{(3-x)^{2}+(4-y)^{2}}$,
∵|AB|=1,∴x2+y2=1,
∴$\sqrt{(3-x)^{2}+(4-y)^{2}}$表示单位圆上的点到M(3,4)的距离,
∴$\sqrt{(3-x)^{2}+(4-y)^{2}}$的最小值为|OM|-1=4,$\sqrt{(3-x)^{2}+(4-y)^{2}}$的最大值为|OM|+1=6,
故选C.
点评 本题考查了平面向量的运算,属于中档题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
14.设{an}是公差不为0的等差数列,满足a42+a52=a62+a72,则{an}的前10项和S10=( )
| A. | -10 | B. | -5 | C. | 0 | D. | 5 |
16.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2},}&{x≤1}\\{x+\frac{4}{x}-3,}&{x>1}\end{array}\right.$,则f(x)的值域是( )
| A. | [1,+∞) | B. | [0,+∞) | C. | (1,+∞) | D. | [0,1)∪(1,+∞) |
13.“a<-2”是“函数y=ax+3在区间(-1,3)上存在零点”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |