题目内容
在△ABC中,内角A,B,C的对边分别为a,b,c,且
=(a,b),
=(sinB,-cosA),且
•
=0.
(1)求内角A的大小;
(2)若a=10,求△ABC面积的最大值.
| m |
| n |
| m |
| n |
(1)求内角A的大小;
(2)若a=10,求△ABC面积的最大值.
考点:余弦定理,平面向量数量积的运算,正弦定理
专题:三角函数的求值
分析:(1)由两向量的坐标,利用平面向量的数量积运算法则列出关系式,再利用正弦定理化简,根据sinB不为0求出tanA的值,即可确定出A的度数;
(2)利用余弦定理列出关系式,将a,cosA的值代入,利用基本不等式求出bc的最大值,即可确定出三角形ABC面积的最大值.
(2)利用余弦定理列出关系式,将a,cosA的值代入,利用基本不等式求出bc的最大值,即可确定出三角形ABC面积的最大值.
解答:
解:(1)∵
=(a,b),
=(sinB,-cosA),且
•
=0,
∴asinB-bcosA=0,
∴由正弦定理得sinAsinB-sinBcosA=0,
∵0<B<π,∴sinB≠0,
∴sinA=cosA,即tanA=1,
∵0<A<π,
∴A=
;
(2)∵a=10,cosA=
,
∴由余弦定理得a2=b2+c2-2bccosA=102,即b2+c2-
bc=100,
∵b2+c2≥2bc,
∴100+
bc≥2bc,
∴100≥(2-
)bc,即bc≤
,
∵S=
bcsinA=
bc≤
×
=25(
+1),
∴当且仅当b=c时,△ABC面积有最大值,最大值为25(
+1).
| m |
| n |
| m |
| n |
∴asinB-bcosA=0,
∴由正弦定理得sinAsinB-sinBcosA=0,
∵0<B<π,∴sinB≠0,
∴sinA=cosA,即tanA=1,
∵0<A<π,
∴A=
| π |
| 4 |
(2)∵a=10,cosA=
| ||
| 2 |
∴由余弦定理得a2=b2+c2-2bccosA=102,即b2+c2-
| 2 |
∵b2+c2≥2bc,
∴100+
| 2 |
∴100≥(2-
| 2 |
| 100 | ||
2-
|
∵S=
| 1 |
| 2 |
| ||
| 4 |
| ||
| 4 |
| 100 | ||
2-
|
| 2 |
∴当且仅当b=c时,△ABC面积有最大值,最大值为25(
| 2 |
点评:此题考查了余弦定理,平面向量的数量积运算,三角形的面积公式,以及基本不等式的运用,熟练掌握定理及公式是解本题的关键.

练习册系列答案
相关题目
若某简单空间几何体的三视图是三个半径为1的圆,则这个空间几何体的表面积为( )
| A、2π | B、4π | C、6π | D、8π |
设l,m,n为不同的直线,α,β为不同的平面,下列命题中正确的是( )
| A、若l∥α,m?α,则l∥m |
| B、若m∥n,n?α,则m∥α |
| C、若α不垂直于β,则α内不存在直线垂直于β |
| D、若α⊥β,l∥α,则l⊥β |
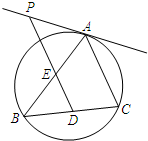 如图,△ABC内接于圆O,D为弦BC上一点,过D作直线DP∥AC,交AB于点E,交圆O
如图,△ABC内接于圆O,D为弦BC上一点,过D作直线DP∥AC,交AB于点E,交圆O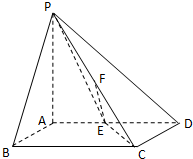 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是正方形,且PA=AD=2,E,F分别是棱AD,PC的中点.
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是正方形,且PA=AD=2,E,F分别是棱AD,PC的中点. 如图,在平面直角坐标系中,直线y=kx+b(k≠0)分别交双曲线
如图,在平面直角坐标系中,直线y=kx+b(k≠0)分别交双曲线