题目内容
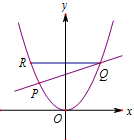
 如图,在平面直角坐标系中,直线y=kx+b(k≠0)分别交双曲线y=
如图,在平面直角坐标系中,直线y=kx+b(k≠0)分别交双曲线y=| m |
| x |
| 4 |
| 5 |
(1)求该双曲线y=
| m |
| x |
(2)连接BC,求△ABC的面积.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程
分析:(1)由于倾斜角∠ADC为锐角,已知sin∠ADC=
,利用三角函数基本关系式可得斜率k.利用CD=4,C(3,0),可得D(-1,0),代入直线AB可得b.进而得到直线AB的方程.把B(-3,n)代入直线AB的方程可得n,可得B并代入双曲线y=
可得m即可.
(2)设A(x,
)(x>0),利用两点间的距离公式和AD=5,可得x.再利用S△ABC=S△ADC+S△BCD=
|DC|•yA+
|DC|•(-yB)即可得出.
| 4 |
| 5 |
| m |
| x |
(2)设A(x,
| 8 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(1)∵sin∠ADC=
,又∠ADC为锐角,
∴cos∠ADC=
=
,
∴tan∠ADC=
=
,
∴斜率k=
.
∴CD=4,C(3,0),∴D(-1,0),
代入直线AB:0=-k+b,∴b=k=
.
∴直线AB的方程为:y=
x+
.
把B(-3,n)代入上式可得:n=-3×
+
=-
.
∴B(-3,-
).
把B的坐标代入双曲线y=
可得:m=-3×(-
)=8.
∴双曲线的方程为:y=
.
综上可得:该双曲线y=
,直线AB的解析式为y=
x+
.
(2)设A(x,
)(x>0),
∵AD=5,∴
=5,解得x=2.
∴A(2,4).∴S△ABC=S△ADC+S△BCD=
|DC|•yA+
|DC|•(-yB)
=
×4×(4+
)=
.
| 4 |
| 5 |
∴cos∠ADC=
| 1-cos2∠ADC |
| 3 |
| 5 |
∴tan∠ADC=
| sin∠ADC |
| cos∠ADC |
| 4 |
| 3 |
∴斜率k=
| 4 |
| 3 |
∴CD=4,C(3,0),∴D(-1,0),
代入直线AB:0=-k+b,∴b=k=
| 4 |
| 3 |
∴直线AB的方程为:y=
| 4 |
| 3 |
| 4 |
| 3 |
把B(-3,n)代入上式可得:n=-3×
| 4 |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
∴B(-3,-
| 8 |
| 3 |
把B的坐标代入双曲线y=
| m |
| x |
| 8 |
| 3 |
∴双曲线的方程为:y=
| 8 |
| x |
综上可得:该双曲线y=
| 8 |
| x |
| 4 |
| 3 |
| 4 |
| 3 |
(2)设A(x,
| 8 |
| x |
∵AD=5,∴
(x+1)2+(
|
∴A(2,4).∴S△ABC=S△ADC+S△BCD=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 8 |
| 3 |
| 40 |
| 3 |
点评:本题考查了三角函数的基本关系式、斜率与倾斜角的关系、直线与双曲线相交问题、两点间的距离公式、三角形的面积计算公式等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
已知i是虚数单位,则
=( )
| 2-i |
| 1+2i |
| A、-i | ||||
B、
| ||||
| C、-1 | ||||
D、
|
y=f(x)是定义在R上的函数,若a∈R,则“x≠a”是“f(x)≠f(a)”成立的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
 如图,设直线l:y=kx+
如图,设直线l:y=kx+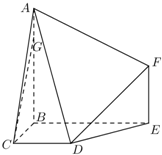 如图,多面体ABCDEF中,BA,BC,BE两两垂直,且AB∥EF,CD∥BE,AB=BE=2,BC=CD=EF=1.
如图,多面体ABCDEF中,BA,BC,BE两两垂直,且AB∥EF,CD∥BE,AB=BE=2,BC=CD=EF=1.