题目内容
已知函数f(x)=
-ax(x>0且x≠1)
(1)若f(x)在定义域上为减函数,求实数a的取值范围;
(2)若有x1、x2∈[e,e2],使f(x1)≤f′(x2)+a成立,求实数a的取值范围.
| x |
| lnx |
(1)若f(x)在定义域上为减函数,求实数a的取值范围;
(2)若有x1、x2∈[e,e2],使f(x1)≤f′(x2)+a成立,求实数a的取值范围.
考点:导数在最大值、最小值问题中的应用
专题:综合题,导数的综合应用
分析:(1)f(x)在定义域上为减函数,f′(x)=
-a≤0,在(0,+∞)上恒成立,分离参数求最值,即可求实数a的取值范围;
(2)命题“若存在x1,x2∈[e,e2],使f(x1)≤f′(x2)+a成立”等价于“当x∈[e,e2]时,有f(x)min≤f′(x)max+a”,求出f′(x)max+a=
,故问题等价于:“当x∈[e,e2]时,有f(x)min≤
,分类讨论,即可求实数a的取值范围.
| lnx-1 |
| (lnx)2 |
(2)命题“若存在x1,x2∈[e,e2],使f(x1)≤f′(x2)+a成立”等价于“当x∈[e,e2]时,有f(x)min≤f′(x)max+a”,求出f′(x)max+a=
| 1 |
| 4 |
| 1 |
| 4 |
解答:
解:(1)∵f(x)在定义域上为减函数,
∴f′(x)=
-a≤0,在(0,+∞)上恒成立,
即当x∈(0,+∞)时,a≥
=-(
-
)2+
即可,
∴a≥
;
(2)命题“若存在x1,x2∈[e,e2],使f(x1)≤f′(x2)+a成立”等价于
“当x∈[e,e2]时,有f(x)min≤f′(x)max+a”,
由(1)得,当x∈[e,e2]时,f′(x)max=
-a,则f′(x)max+a=
,
故问题等价于:“当x∈[e,e2]时,有f(x)min≤
.
当a≥
时,f(x)在[e,e2]上为减函数,则f(x)min=f(e2)=
-ae2≤
.
∴a≥
-
.
a≤0,f′(x)≥0在[e,e2]恒成立,故f(x)在[e,e2]上为增函数,
于是,f(x)min=f(e)=e-ae≥e>
,不合题意
0<a<
时,由f′(x)的单调性和值域知,存在唯一x0∈(e,e2),使f′(x0)=0,且满足:
当x∈(e,x0)时,f′(x)<0,f(x)为减函数;当x∈(x0,e2)时,f′(x)>0,f(x)为增函数;
∴f(x)min=f(x0),
∴a≥
-
>
-
>
,与0<a<
矛盾,
综上,a≥
-
.
∴f′(x)=
| lnx-1 |
| (lnx)2 |
即当x∈(0,+∞)时,a≥
| lnx-1 |
| (lnx)2 |
| 1 |
| lnx |
| 1 |
| 2 |
| 1 |
| 4 |
∴a≥
| 1 |
| 4 |
(2)命题“若存在x1,x2∈[e,e2],使f(x1)≤f′(x2)+a成立”等价于
“当x∈[e,e2]时,有f(x)min≤f′(x)max+a”,
由(1)得,当x∈[e,e2]时,f′(x)max=
| 1 |
| 4 |
| 1 |
| 4 |
故问题等价于:“当x∈[e,e2]时,有f(x)min≤
| 1 |
| 4 |
当a≥
| 1 |
| 4 |
| e2 |
| 2 |
| 1 |
| 4 |
∴a≥
| 1 |
| 2 |
| 1 |
| 4e2 |
a≤0,f′(x)≥0在[e,e2]恒成立,故f(x)在[e,e2]上为增函数,
于是,f(x)min=f(e)=e-ae≥e>
| 1 |
| 4 |
0<a<
| 1 |
| 4 |
当x∈(e,x0)时,f′(x)<0,f(x)为减函数;当x∈(x0,e2)时,f′(x)>0,f(x)为增函数;
∴f(x)min=f(x0),
∴a≥
| 1 |
| lnx0 |
| 1 |
| 4x0 |
| 1 |
| lne |
| 1 |
| 4e2 |
| 1 |
| 4 |
| 1 |
| 4 |
综上,a≥
| 1 |
| 2 |
| 1 |
| 4e2 |
点评:本题考查导数知识的综合运用,考查函数的最值,考查恒成立问题,考查分类讨论的数学思想,难度大.

练习册系列答案
相关题目
已知p={x|y=
},Q={y|y=-x2+2x+1,x∈N},则P∩Q=( )
| x+1 |
| A、{1,2} |
| B、{x|-1≤x≤2} |
| C、{0,1,2} |
| D、∅ |
下面程序输出结果是( )


| A、1,1 | B、2,1 |
| C、1,2 | D、2,2 |
y=f(x)是定义在R上的函数,若a∈R,则“x≠a”是“f(x)≠f(a)”成立的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
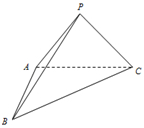 如图,在三棱锥P-ABC中,AB⊥AC,PA=PB=PC=3,AB=2
如图,在三棱锥P-ABC中,AB⊥AC,PA=PB=PC=3,AB=2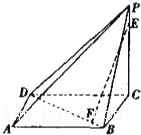 已知四棱锥P-ABCD中,PC⊥底面ABCD,PC=2,且底面ABCD是边长为1的正方形.E是最短的侧棱PC上的动点.
已知四棱锥P-ABCD中,PC⊥底面ABCD,PC=2,且底面ABCD是边长为1的正方形.E是最短的侧棱PC上的动点.