题目内容
若某简单空间几何体的三视图是三个半径为1的圆,则这个空间几何体的表面积为( )
| A、2π | B、4π | C、6π | D、8π |
考点:简单空间图形的三视图
专题:计算题
分析:几何体是半径为1的球,利用球的表面积公式计算可得答案.
解答:
解:根据几何体的三视图是三个半径为1的圆,得几何体是半径为1的球,
∴几何体的表面积S=4π×12=4π.
故选:B.
∴几何体的表面积S=4π×12=4π.
故选:B.
点评:本题考查了由三视图求几何体的表面积,判断几何体的形状是关键.

练习册系列答案
相关题目
已知p={x|y=
},Q={y|y=-x2+2x+1,x∈N},则P∩Q=( )
| x+1 |
| A、{1,2} |
| B、{x|-1≤x≤2} |
| C、{0,1,2} |
| D、∅ |
如图所示的算法框图中,语句“输出i”被执行的次数为( )


| A、32 | B、33 | C、34 | D、35 |
阅读如图的程序框图,运行相应的程序,则输出的结果是( )


| A、6 | B、5 | C、4 | D、3 |
如图是计算
+
+
+…+
的值的一个程序框图,其中在判断框中应填入的条件是( )

| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 20 |

| A、i<10 | B、i>10 |
| C、i<20 | D、i>20 |
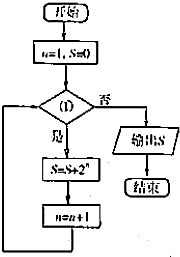 运行如图框图输出的S是254,则①应为
运行如图框图输出的S是254,则①应为