题目内容
 如图,现有一块半径为2m,圆心角为90°的扇形铁皮AOB,欲从其中裁剪出一块内接五边形ONPQR,使点P在AB弧上,点M,N分别在半径OA和OB上,四边形PMON是矩形,点Q在弧AP上,R点在线段AM上,四边形PQRM是直角梯形.现有如下裁剪方案:先使矩形PMON的面积达到最大,在此前提下,再使直角梯形PQRM的面积也达到最大:求出裁剪出的五边形的面积.
如图,现有一块半径为2m,圆心角为90°的扇形铁皮AOB,欲从其中裁剪出一块内接五边形ONPQR,使点P在AB弧上,点M,N分别在半径OA和OB上,四边形PMON是矩形,点Q在弧AP上,R点在线段AM上,四边形PQRM是直角梯形.现有如下裁剪方案:先使矩形PMON的面积达到最大,在此前提下,再使直角梯形PQRM的面积也达到最大:求出裁剪出的五边形的面积.考点:弧度制的应用
专题:圆锥曲线的定义、性质与方程
分析:①设∠PON=θ,则ON=OPcosθ,PN=OPsinθ.可得矩形PMON的面积S=2cosθ•2sinθ=2sin2θ,可得当θ=45°时,此时矩形PMON的面积最大.
②如图所示,设∠QOE=α,(45°<α<90°).作QE⊥OB,垂足为E,交MP于点F.QE=OQsinα=2sinα,OE=OQcosα=2cosα.可得直角梯形PQRM的面积S=
=
=
(4sinαcosα+2
sinα-2
cosα-2).令t=sinα-cosα,t∈(0,1).可得S(t)=
(2-2t2+2
t-2)=-(t-
)2+
,即可得出最大值.
②如图所示,设∠QOE=α,(45°<α<90°).作QE⊥OB,垂足为E,交MP于点F.QE=OQsinα=2sinα,OE=OQcosα=2cosα.可得直角梯形PQRM的面积S=
| (QR+MP)×RM |
| 2 |
=
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
解答:
解:①设∠PON=θ,则ON=OPcosθ,PN=OPsinθ.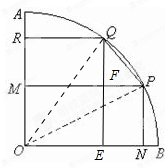
∴矩形PMON的面积S=2cosθ•2sinθ=2sin2θ≤2,当θ=45°时,此时矩形PMON的面积最大为2.
②如图所示,设∠QOE=α,(45°<α<90°).
作QE⊥OB,垂足为E,交MP于点F.
QE=OQsinα=2sinα,OE=OQcosα=2cosα.
∴RM=QE-EF=2sinα-
.
∴直角梯形PQRM的面积S=
=
=
(4sinαcosα+2
sinα-2
cosα-2).
令t=sinα-cosα,t∈(0,1).
则t2=1-2sinαcosα,可得sinαcosα=
.
∴S(t)=
(2-2t2+2
t-2)=-(t-
)2+
,
∴当t=
时,S(t)取得最大值
,此时
=
sin(α-45°),解得α=75°.
∴裁剪出的五边形的面积=2+
=
.

∴矩形PMON的面积S=2cosθ•2sinθ=2sin2θ≤2,当θ=45°时,此时矩形PMON的面积最大为2.
②如图所示,设∠QOE=α,(45°<α<90°).
作QE⊥OB,垂足为E,交MP于点F.
QE=OQsinα=2sinα,OE=OQcosα=2cosα.
∴RM=QE-EF=2sinα-
| 2 |
∴直角梯形PQRM的面积S=
| (QR+MP)×RM |
| 2 |
(2cosα+
| ||||
| 2 |
=
| 1 |
| 2 |
| 2 |
| 2 |
令t=sinα-cosα,t∈(0,1).
则t2=1-2sinαcosα,可得sinαcosα=
| 1-t2 |
| 2 |
∴S(t)=
| 1 |
| 2 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
∴当t=
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 2 |
∴裁剪出的五边形的面积=2+
| 1 |
| 2 |
| 5 |
| 2 |
点评:本题考查了圆心角为90°的扇形铁皮AOB中裁剪出一块内接五边形ONPQR的面积最大值问题,考查了三角函数的变换及其单调性,考查了矩形与直角梯形面积的最大值问题,考查了推理能力与计算能力,属于难题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
函数f(x)=x5+x-3的零点的个数是( )
| A、0 | B、1 | C、2 | D、3 |
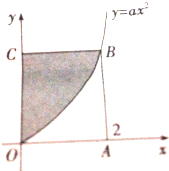 如图,长方形的四个顶点为O(0,0),A(2,0),B(2,4),C(0,4)曲线y=ax2经过点B,现将一质点随机投入正方形OABC中,则质点落在图中阴影区域的概率是
如图,长方形的四个顶点为O(0,0),A(2,0),B(2,4),C(0,4)曲线y=ax2经过点B,现将一质点随机投入正方形OABC中,则质点落在图中阴影区域的概率是