题目内容
已知函数f(x)=(x2-2x)lnx+ax2+2.
(Ⅰ)当a=-1时,求f(x)在点(1,f(1))处的切线方程;
(Ⅱ)当a>0时,设函数g(x)=f(x)-x-2,且函数g(x)有且仅有一个零点,若e-2<x<e,g(x)≤m,求m的取值范围.
(Ⅰ)当a=-1时,求f(x)在点(1,f(1))处的切线方程;
(Ⅱ)当a>0时,设函数g(x)=f(x)-x-2,且函数g(x)有且仅有一个零点,若e-2<x<e,g(x)≤m,求m的取值范围.
考点:利用导数研究曲线上某点切线方程,函数零点的判定定理
专题:导数的综合应用
分析:(Ⅰ)当a=-1时,求导数,可得切线斜率,求出切点坐标,即可求f(x)在(1,f(1))处的切线方程;
(Ⅱ)由g(x)=f(x)-x-2=0,可得a=
,令h(x)=
,证明h(x)在(0,1)上单调递增,在(1,+∞)上单调递减,可得h(x)max=h(1)=1,即可求得函数g(x)有且仅有一个零点a的值,然后结合e-2<x<e,g(x)≤m,求出g(x)max,即可求得m的取值范围.
(Ⅱ)由g(x)=f(x)-x-2=0,可得a=
| 1-(x-2)lnx |
| x |
| 1-(x-2)lnx |
| x |
解答:
解:(Ⅰ)当a=-1时,f(x)=(x2-2x)•lnx-x2+2,定义域(0,+∞),
∴f′(x)=(2x-2)•lnx+(x-2)-2x.
∴f′(1)=-3,
又f(1)=1,
∴f(x)在(1,f(1))处的切线方程3x+y-4=0;
(Ⅱ)g(x)=f(x)-x-2=0,
则(x2-2x)•lnx+ax2+2=x+2,即a=
,
令h(x)=
,
则h′(x)=
,令t(x)=1-x-2lnx,则t′(x)=
,
∵x>0,∴t′(x)<0,
∴t(x)在(0,+∞)上是减函数,
又∵t(1)=h′(1)=0,
∴当0<x<1时,h′(x)>0,当x>1时,h′(x)<0,
∴h(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
∴h(x)max=h(1)=1,
∴当函数g(x)有且仅有一个零点时a=1,
当a=1时,g(x)=(x2-2x)•lnx+x2-x,
若e-2<x<e,g(x)≤m,只需证明g(x)max≤m,
∴g′(x)=(x-1)(3+2lnx),
令g′(x)=0,得x=1或x=e-
,
又∵e-2<x<e,
∴函数g(x)在(e-2,e-
)上单调递增,在(e-
,1)上单调递减,在(1,e)上单调递增,
又g(e-
)=-
e-3+2e-
,g(e)=2e2-3e,
∵g(e-
)=-
e-3+2e-
<2e-
<2e<2e(e-
)=g(e),
∴g(e-
)<g(e),
∴m≥2e2-3e.
∴f′(x)=(2x-2)•lnx+(x-2)-2x.
∴f′(1)=-3,
又f(1)=1,
∴f(x)在(1,f(1))处的切线方程3x+y-4=0;
(Ⅱ)g(x)=f(x)-x-2=0,
则(x2-2x)•lnx+ax2+2=x+2,即a=
| 1-(x-2)lnx |
| x |
令h(x)=
| 1-(x-2)lnx |
| x |
则h′(x)=
| 1-x-2lnx |
| x2 |
| -x-2 |
| x |
∵x>0,∴t′(x)<0,
∴t(x)在(0,+∞)上是减函数,
又∵t(1)=h′(1)=0,
∴当0<x<1时,h′(x)>0,当x>1时,h′(x)<0,
∴h(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
∴h(x)max=h(1)=1,
∴当函数g(x)有且仅有一个零点时a=1,
当a=1时,g(x)=(x2-2x)•lnx+x2-x,
若e-2<x<e,g(x)≤m,只需证明g(x)max≤m,
∴g′(x)=(x-1)(3+2lnx),
令g′(x)=0,得x=1或x=e-
| 3 |
| 2 |
又∵e-2<x<e,
∴函数g(x)在(e-2,e-
| 3 |
| 2 |
| 3 |
| 2 |
又g(e-
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∵g(e-
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
∴g(e-
| 3 |
| 2 |
∴m≥2e2-3e.
点评:本题考查导数知识的综合运用,考查导数的几何意义,考查函数的单调性与最值,考查分离参数法的运用,属于难题.

练习册系列答案
相关题目
若函数f(x)=
x3+x2-
在区间(a,a+5)内存在最小值,则实数a的取值范围是( )
| 1 |
| 3 |
| 2 |
| 3 |
| A、[-5,0) |
| B、(-5,0) |
| C、[-3,0) |
| D、(-3,0) |
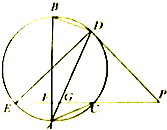 如图所示,EP交圆于E,C两点,PD切圆于D,G为CE上一点且PG=PD,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.
如图所示,EP交圆于E,C两点,PD切圆于D,G为CE上一点且PG=PD,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F. 如图,现有一块半径为2m,圆心角为90°的扇形铁皮AOB,欲从其中裁剪出一块内接五边形ONPQR,使点P在AB弧上,点M,N分别在半径OA和OB上,四边形PMON是矩形,点Q在弧AP上,R点在线段AM上,四边形PQRM是直角梯形.现有如下裁剪方案:先使矩形PMON的面积达到最大,在此前提下,再使直角梯形PQRM的面积也达到最大:求出裁剪出的五边形的面积.
如图,现有一块半径为2m,圆心角为90°的扇形铁皮AOB,欲从其中裁剪出一块内接五边形ONPQR,使点P在AB弧上,点M,N分别在半径OA和OB上,四边形PMON是矩形,点Q在弧AP上,R点在线段AM上,四边形PQRM是直角梯形.现有如下裁剪方案:先使矩形PMON的面积达到最大,在此前提下,再使直角梯形PQRM的面积也达到最大:求出裁剪出的五边形的面积.