题目内容
已知向量
=(x,4y+4),向量
=(x,y-1),且
⊥
,动点M(x,y)的轨迹为E,
(1)求轨迹E的方程;
(2)证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且OA⊥OB(O为坐标原点),并求出该圆的方程.
| a |
| b |
| a |
| b |
(1)求轨迹E的方程;
(2)证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且OA⊥OB(O为坐标原点),并求出该圆的方程.
考点:圆与圆锥曲线的综合,圆的标准方程,轨迹方程
专题:综合题,转化思想
分析:(1)已知两向量的坐标和两向量的内积为0,有内积的坐标表示法即可得动点M的轨迹方程;
(2)由题意对于要找的直线分斜率存在与不存在加以讨论,对于斜率存在设出直线与动点轨迹E进行联立,利用根与系数的关系及方程的思想求出要求的圆的方程;对于斜率不存在点都具体加以验证即可.
(2)由题意对于要找的直线分斜率存在与不存在加以讨论,对于斜率存在设出直线与动点轨迹E进行联立,利用根与系数的关系及方程的思想求出要求的圆的方程;对于斜率不存在点都具体加以验证即可.
解答:
解:(1)因为
⊥
,
=(x,4y+4),
=(x,y-1),
所以
•
=x2+4(y2-1)=0,所以,轨迹E的方程为:
+y2=1;
(2)设圆心在原点的圆的一条切线为y=kx+t,
解方程组
得x2+4(kx+t)2=4,
即(1+4k2)x2+8ktx+4t2-4=0
要使切线与轨迹E恒有两个交点A,B
则使△=64k2t2-16(1+4k2)(t2-1)=16(4k2-t2+1)>0
即:4k2-t2+1>0,即t2<4k2+1
且
y1y2=(kx1+t)(kx2+t)=k2x1x2+kt(x1+x2)+t2=
-
+t2=
要使
⊥
,需使x1x2+y1y2=0
即:
+
=
=0
所以5t2-4k2-4=0
即5t2=4k2+4且t2<4k2+1
即4k2+4<20k2+5
即16k2>-1,恒成立.
又因为直线y=kx+t为圆心在原点的圆的一条切线
所以圆半径为r=
,r2=
=
=
,所求的圆为x2+y2=
当切线的斜率不存在时,切线为x=±
,与
+y2=1交于点(
,±
)或(-
,±
或(-
,±
)也满足OA⊥OB
综上所述,存在圆心在原点的圆x2+y2=
使得该圆的任意一条切线与椭圆E恒有两个交点.
| a |
| b |
| a |
| b |
所以
| a |
| b |
| x2 |
| 4 |
(2)设圆心在原点的圆的一条切线为y=kx+t,
解方程组
|
即(1+4k2)x2+8ktx+4t2-4=0
要使切线与轨迹E恒有两个交点A,B
则使△=64k2t2-16(1+4k2)(t2-1)=16(4k2-t2+1)>0
即:4k2-t2+1>0,即t2<4k2+1
且
|
y1y2=(kx1+t)(kx2+t)=k2x1x2+kt(x1+x2)+t2=
| k2(4t2-4) |
| 1+4k2 |
| 8k2t2 |
| 1+4k2 |
| t2-4k2 |
| 1+4k2 |
要使
. |
| OA |
. |
| OB |
即:
| 4t2-4 |
| 1+4k2 |
| t2-4k2 |
| 1+4k2 |
| 5t2-4k2-4 |
| 1+4k2 |
所以5t2-4k2-4=0
即5t2=4k2+4且t2<4k2+1
即4k2+4<20k2+5
即16k2>-1,恒成立.
又因为直线y=kx+t为圆心在原点的圆的一条切线
所以圆半径为r=
| |t| | ||
|
| t2 |
| 1+k2 |
| ||
| 1+k2 |
| 4 |
| 5 |
| 4 |
| 5 |
当切线的斜率不存在时,切线为x=±
| 2 |
| 5 |
| 5 |
| x2 |
| 4 |
| 2 |
| 5 |
| 5 |
| 2 |
| 5 |
| 5 |
| 2 |
| 5 |
| 5 |
| 2 |
| 5 |
| 5 |
| 2 |
| 5 |
| 5 |
| 2 |
| 5 |
| 5 |
综上所述,存在圆心在原点的圆x2+y2=
| 4 |
| 5 |
点评:此题第一问重点考查了两向量的内积的坐标的表示方法,还考查了直接法求动点的轨迹的方法;第二问重点考查了直线方程与椭圆方程进行联立后根与系数的关系及设而不求和整体代换的思想,还考查了分析问题时的分类讨论的问题.

练习册系列答案
相关题目
在任意的三个整数中,有且只有一个偶数的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
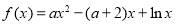 .
.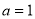 时,求曲线
时,求曲线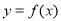 在点
在点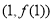 处的切线方程;
处的切线方程;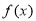 的单调区间;
的单调区间;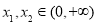 ,
,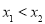 ,且
,且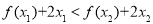 恒成立,求
恒成立,求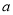 的取值范围.
的取值范围.