题目内容
(本小题满分14分)已知函数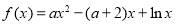 .
.
(Ⅰ)当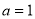 时,求曲线
时,求曲线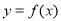 在点
在点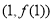 处的切线方程;
处的切线方程;
(Ⅱ)求函数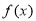 的单调区间;
的单调区间;
(Ⅲ)若对任意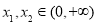 ,
,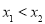 ,且
,且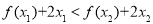 恒成立,求
恒成立,求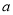 的取值范围.
的取值范围.
 ,
,


0<a≤8
【解析】
试题分析:定义域:
(Ⅰ)当a=1时, ,
, ,所以在点
,所以在点 处的切线斜率为
处的切线斜率为 ,所以切线为:
,所以切线为:
(Ⅱ)
 两根为
两根为




(Ⅲ)设g(x)=f(x)+2x,则g(x)=ax2-ax+lnx,
只要g(x)在(0,+∞)上单调递增即可,
而g′(x)=2ax-a+ =
=
当a=0时,g′(x)=  >0,此时g(x)在(0,+∞)上单调递增;
>0,此时g(x)在(0,+∞)上单调递增;
当a≠0时,只需g′(x)≥0在(0,+∞)上恒成立,
因为x∈(0,+∞),只要2ax2-ax+1≥0,
则需要a>0,
对于函数y=2ax2-ax+1,过定点(0,1),对称轴x=  >0,只需△=a2-8a≤0,即0<a≤8,
>0,只需△=a2-8a≤0,即0<a≤8,
考点:本题考查导函数

练习册系列答案
相关题目
a≥0,b≥0,a+b=1,且x1,x2为正数,y1=ax1+bx2,y2=bx1+ax2,则y1y2与x1x2的大小关系是( )
| A、y1y2≥x1x2 |
| B、y1y2≤x1x2 |
| C、y1y2>x1x2 |
| D、y1y2<x1x2 |
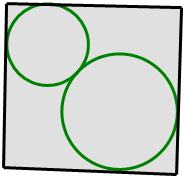 如图,在单位正方形内作两个互相外切的圆,同时每一个圆又与正方形的两相邻边相切,记其中一个圆的半径为x,两圆的面积之和为S,将S表示为x的函数,求函数S=f(x)的解析式及f(x)的值域.
如图,在单位正方形内作两个互相外切的圆,同时每一个圆又与正方形的两相邻边相切,记其中一个圆的半径为x,两圆的面积之和为S,将S表示为x的函数,求函数S=f(x)的解析式及f(x)的值域. ,
, ,则
,则 所表示的区域的面积为________;
所表示的区域的面积为________;  所表示的区域的面积为 .
所表示的区域的面积为 . 、
、 满足
满足 ,则
,则 的最小值为( )
的最小值为( ) (C)
(C) (D)
(D)

 ,则
,则 的值为 .
的值为 .