题目内容
若关于x的方程x2-ax+a2-3=0至少有一个正根,则实数a的取值范围是 .
考点:一元二次方程的根的分布与系数的关系
专题:计算题
分析:关于x的方程x2-ax+a2-3=0至少有一个正根?(1)当方程只有一个根,且为正根,(2)当方程有两个根
①方程的两个根中只有一个正根,一个复根或零根,②若方程有两个正根,结合二次方程的根的情况可求.
①方程的两个根中只有一个正根,一个复根或零根,②若方程有两个正根,结合二次方程的根的情况可求.
解答:
解:∵△=a2-4(a2-3)=12-3a2
(1)当方程只有一个根时,△=0,此时a=±2
若a=2,此时方程x2-2x+1=0的根x=1符合条件
若a=-2,此时方程x2+2x+1=0的根x=-1不符舍去
(2)当方程有两个根时,△>0可得-2<a<2
①若方程的两个根中只有一个正根,一个负根或零根,则有a2-3≤0,解可得-
≤a≤
,符合条件
②若方程有两个正根,则
,解可得a>
综上可得,-
≤a≤2
故答案为:[-
,2]
(1)当方程只有一个根时,△=0,此时a=±2
若a=2,此时方程x2-2x+1=0的根x=1符合条件
若a=-2,此时方程x2+2x+1=0的根x=-1不符舍去
(2)当方程有两个根时,△>0可得-2<a<2
①若方程的两个根中只有一个正根,一个负根或零根,则有a2-3≤0,解可得-
| 3 |
| 3 |
②若方程有两个正根,则
|
| 3 |
综上可得,-
| 3 |
故答案为:[-
| 3 |
点评:本题考查一元二次方程的根的分布与系数的关系,考查分类讨论思想,转化思想,是中档题.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
当
<x<
时,函数f(x)=
的最小值是( )
| π |
| 4 |
| π |
| 2 |
| sin2x |
| 2cosx(sinx-cosx) |
| A、2 | ||
| B、1 | ||
C、
| ||
D、
|
若
=b,则a+b=( )
| lim |
| x→1 |
| x+a | |||
|
| A、-2 | B、0 | C、2 | D、4 |

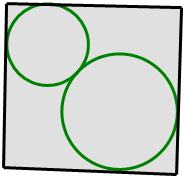 如图,在单位正方形内作两个互相外切的圆,同时每一个圆又与正方形的两相邻边相切,记其中一个圆的半径为x,两圆的面积之和为S,将S表示为x的函数,求函数S=f(x)的解析式及f(x)的值域.
如图,在单位正方形内作两个互相外切的圆,同时每一个圆又与正方形的两相邻边相切,记其中一个圆的半径为x,两圆的面积之和为S,将S表示为x的函数,求函数S=f(x)的解析式及f(x)的值域.