题目内容
已知数列{an}满足a1=2,a2=3,2an+1=3an-an-1(n∈N*且n≥2),若bn+1=an+1-an,
(Ⅰ)证明:数列{bn}为等比数列,并求数列{an}的通项公式.
(Ⅱ)求使不等式
<
成立的所有正整数m,n的值.
(Ⅰ)证明:数列{bn}为等比数列,并求数列{an}的通项公式.
(Ⅱ)求使不等式
| an-m |
| an+1-m |
| 2 |
| 3 |
考点:数列与不等式的综合
专题:常规题型,压轴题,分类讨论
分析:(I)利用数列{bn}与数列{an}项之间的关系整体找寻相邻项之间的关系是解决本题的关键,先求出等比数列{bn}的通项公式,在利用数列{bn}与数列{an}项之间的关系确定出数列{an}的通项公式;
(II)利用相邻项之间的关系,将所求解的不等式进行转化变形是解决本题的关键.通过数列的单调性转化为整数m与数列项的关系进一步确定出所有正整数m,n的值.
(II)利用相邻项之间的关系,将所求解的不等式进行转化变形是解决本题的关键.通过数列的单调性转化为整数m与数列项的关系进一步确定出所有正整数m,n的值.
解答:
解:(I)由2an+1=3an-an-1变形得2an+1-2an=an-an-1(n≥2),故2bn+1=bn
故{bn}是以a2-a1为首项,
为公比的等比数列.
an+1-an=(
)n-1
由累加法得an-a1=
,故an=4-(
)n-2.
(II)要使不等式
<
则
-
<0,∴
<0
又2an+1=3an-an-1,则有
<0,(n≥2)
又an=4-(
)n-2是单调递增数列,故an+1>an-1
∴an+1>m>an-1(n≥2),即
当n=2,解得2<m<3.5.即m=3.
当n≥3时,
,即3<m<4,不合题意.
另当n=1,
<
,
<0,解得0<m<3,即得m=1,2
总上所述:满足条件的正整数m,n为:
当n=1,m=1或2,当n=2时,m=3.
故{bn}是以a2-a1为首项,
| 1 |
| 2 |
an+1-an=(
| 1 |
| 2 |
由累加法得an-a1=
1-(
| ||
1-
|
| 1 |
| 2 |
(II)要使不等式
| an-m |
| an+1-m |
| 2 |
| 3 |
| an-m |
| an+1-m |
| 2 |
| 3 |
| 3an-3m-2an+1+2m |
| 3(an+1-m) |
又2an+1=3an-an-1,则有
| an-1-m |
| an+1-m |
又an=4-(
| 1 |
| 2 |
∴an+1>m>an-1(n≥2),即
|
当n≥3时,
|
另当n=1,
| an-m |
| an+1-m |
| 2 |
| 3 |
| a 1-m |
| a2-m |
总上所述:满足条件的正整数m,n为:
当n=1,m=1或2,当n=2时,m=3.
点评:本题考查数列的递推关系确定数列通项公式的方法,利用整体思想确定出数列满足的递推关系,从而确定数列是哪一类特殊数列.考查学生的累加法求通项公式.考查学生分式不等式的求解方法,体现解题的转化与化归思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 如图,是一个奖杯的三视图(单位:cm),底座是正四棱台
如图,是一个奖杯的三视图(单位:cm),底座是正四棱台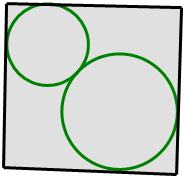 如图,在单位正方形内作两个互相外切的圆,同时每一个圆又与正方形的两相邻边相切,记其中一个圆的半径为x,两圆的面积之和为S,将S表示为x的函数,求函数S=f(x)的解析式及f(x)的值域.
如图,在单位正方形内作两个互相外切的圆,同时每一个圆又与正方形的两相邻边相切,记其中一个圆的半径为x,两圆的面积之和为S,将S表示为x的函数,求函数S=f(x)的解析式及f(x)的值域. 、
、 满足
满足 ,则
,则 的最小值为( )
的最小值为( ) (C)
(C) (D)
(D)