题目内容
已知集合A={x|x2-5x-6＜0}，B={x||x|＜2}，则A∩（∁RB）=（ ）
| A、（-1，2） |
| B、[-1，2） |
| C、（2，6） |
| D、[2，6） |
考点：交、并、补集的混合运算
专题：集合
分析：分别求出A与B中不等式的解集确定出两集合，根据全集R求出B的补集，找出A与B补集的交集即可．
解答：
解：由A中的不等式变形得：（x-6）（x+1）＜0，
解得：-1＜x＜6，即A=（-1，6）；
由B中的不等式变形得：-2＜x＜2，即B=（-2，2），
∵全集为R，
∴∁RB=（-∞，-2]∪[2，+∞），
则A∩（∁RB）=[2，6）．
故选：D．
解得：-1＜x＜6，即A=（-1，6）；
由B中的不等式变形得：-2＜x＜2，即B=（-2，2），
∵全集为R，
∴∁RB=（-∞，-2]∪[2，+∞），
则A∩（∁RB）=[2，6）．
故选：D．
点评：此题考查了交、并、补集的混合运算，熟练掌握各自的定义是解本题的关键．
练习册系列答案
相关题目
已知异面直线a、b的方向向量分别为
、
，平面α、β的法向量分别为
、
，则下列命题中是假命题的是（ ）
| a |
| b |
| m |
| n |
A、对于
| ||||||||||||||
B、若
| ||||||||||||||
C、若cos＜
| ||||||||||||||
D、若二面角α-l-β的大小为γ，则γ=＜
|
已知f(x)=
定义域为M，g（x）=ex值域为N，则M∩N=（ ）
| 1-x |
| A、[0，1] |
| B、（0，1] |
| C、（0，+∞） |
| D、[1，+∞） |
焦点在y轴上的双曲线的一条渐近线方程是x-
y=0，此双曲线的离心率为（ ）
| 3 |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
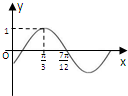已知函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜| π |
| 2 |
| π |
| 6 |
A、{x|x=kπ-
| ||
B、{x|x=kπ-
| ||
C、{x|x=2kπ-
| ||
D、{x|x=2kπ-
|
在平面直角坐标系中，O为坐标原点，点A（2，0），将向量
绕点O按逆时针方向旋转
后得向量
，若向量
满足|
-
-
|=1，则|
|的最大值是（ ）
| OA |
| π |
| 3 |
| OB |
| a |
| a |
| OA |
| OB |
| a |
A、2
| ||||
B、2
| ||||
| C、3 | ||||
D、
|