题目内容
f(x)=|x-3|+|x|+|x-5|+|x+7|+|x+4|,求此函数的值域.
考点:函数的值域
专题:分类法
分析:对自变量x取值进行讨论,去绝对值,再求值域.
解答:
解:f(x)=
,∵f(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增,
∴f(x)≥19,即函数的值域为[19,+∞).
故答案为:[19,+∞).
|
∴f(x)≥19,即函数的值域为[19,+∞).
故答案为:[19,+∞).
点评:函数的图象是连续不断的,所以在后面不需要在每一段上求出y的范围,再求并集,直接根据单调性求就行.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
焦点在y轴上的双曲线的一条渐近线方程是x-
y=0,此双曲线的离心率为( )
| 3 |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
在平面直角坐标系中,O为坐标原点,点A(2,0),将向量
绕点O按逆时针方向旋转
后得向量
,若向量
满足|
-
-
|=1,则|
|的最大值是( )
| OA |
| π |
| 3 |
| OB |
| a |
| a |
| OA |
| OB |
| a |
A、2
| ||||
B、2
| ||||
| C、3 | ||||
D、
|
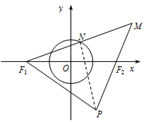 如图,已知定点F1(-2,0),F2(2,0),动点N满足|
如图,已知定点F1(-2,0),F2(2,0),动点N满足| 如图,AB是的⊙O直径,CB与⊙O相切于B,E为线段CB上一点,连接AC、AE分别交⊙O于D、G两点,连接DG交CB于点F.
如图,AB是的⊙O直径,CB与⊙O相切于B,E为线段CB上一点,连接AC、AE分别交⊙O于D、G两点,连接DG交CB于点F.