题目内容
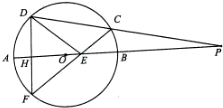 已知:如图,P是⊙O的直径AB延长线上的一点,割线PCD交⊙O于C、D两点,弦DF与直线AB垂直,H为垂足,CF与AB交于点E.
已知:如图,P是⊙O的直径AB延长线上的一点,割线PCD交⊙O于C、D两点,弦DF与直线AB垂直,H为垂足,CF与AB交于点E.(1)求证:PA•PB=PO•PE;
(2)若DE⊥CF,∠P=15°,⊙O的半径等于2,求弦CF的长.
考点:与圆有关的比例线段
专题:
分析:(1)根据切割线定理,PD•PC=PA•PB,所以原题可转化为证明PO•PE=PD•PC,即证△DPO∽△EPC,从而找出比例线段,得到等积式;
(2)由图可知,CF=CE+EF,而由垂径定理可知DE=EF,所以只要求出DE和CE即可,欲求CE,可通过证明△DHO∽△DEC,运用比例线段进行求解,至于DE,则根据题中给出的已知条件可说明三角形DHE为等腰直角三角形,而DH和HE则可通过勾股定理求出,从而求出CF的值.
(2)由图可知,CF=CE+EF,而由垂径定理可知DE=EF,所以只要求出DE和CE即可,欲求CE,可通过证明△DHO∽△DEC,运用比例线段进行求解,至于DE,则根据题中给出的已知条件可说明三角形DHE为等腰直角三角形,而DH和HE则可通过勾股定理求出,从而求出CF的值.
解答:
(1)证明:连接OD.
∵AB是⊙O的直径,且DF⊥AB于D点H,
∴
=
=
.∴∠AOD=∠DCF.∴∠POD=∠PCE.
∵∠DPO=∠EPC,∴△DPO∽△EPC.
∴
=
.即PO•PE=PD•PC.
又PD•PC=PA•PB,∴PA•PB=PO•PE.
(2)解:由(1)知:AB是弦DF的垂直平分线,
∴DE=EF.∴∠DEA=∠FEA.
∵DE⊥CF,∴∠DEA=∠FEA=45°.∴∠FEA=∠CEP=45°.
∵∠P=15°,∴∠AOD=60°.
在Rt△DHO中∵∠AOD=60°,OD=2,
∴OH=1,DH=
.
∵△DHE是等腰直角三角形,∴DE=
.
又∵∠AOD=∠DCF,∠DHO=∠DEC=90°,
∴△DHO∽△DEC.
∴
=
,∴
=
.∴EC=
.
∴CF=CE+EF=CE+DE=
+
.
∵AB是⊙O的直径,且DF⊥AB于D点H,
∴
 |
| AD |
 |
| AF |
| 1 |
| 2 |
 |
| DF |
∵∠DPO=∠EPC,∴△DPO∽△EPC.
∴
| PD |
| PE |
| PO |
| PC |
又PD•PC=PA•PB,∴PA•PB=PO•PE.
(2)解:由(1)知:AB是弦DF的垂直平分线,
∴DE=EF.∴∠DEA=∠FEA.
∵DE⊥CF,∴∠DEA=∠FEA=45°.∴∠FEA=∠CEP=45°.
∵∠P=15°,∴∠AOD=60°.
在Rt△DHO中∵∠AOD=60°,OD=2,
∴OH=1,DH=
| 3 |
∵△DHE是等腰直角三角形,∴DE=
| 6 |
又∵∠AOD=∠DCF,∠DHO=∠DEC=90°,
∴△DHO∽△DEC.
∴
| DH |
| DE |
| HO |
| EC |
| ||
|
| 1 |
| EC |
| 2 |
∴CF=CE+EF=CE+DE=
| 2 |
| 6 |
点评:此题考查比较全面,相似三角形的判定和判定、勾股定理、以及垂径定理,难易程度适中.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
在平面直角坐标系中,O为坐标原点,点A(2,0),将向量
绕点O按逆时针方向旋转
后得向量
,若向量
满足|
-
-
|=1,则|
|的最大值是( )
| OA |
| π |
| 3 |
| OB |
| a |
| a |
| OA |
| OB |
| a |
A、2
| ||||
B、2
| ||||
| C、3 | ||||
D、
|
 如图,AB是的⊙O直径,CB与⊙O相切于B,E为线段CB上一点,连接AC、AE分别交⊙O于D、G两点,连接DG交CB于点F.
如图,AB是的⊙O直径,CB与⊙O相切于B,E为线段CB上一点,连接AC、AE分别交⊙O于D、G两点,连接DG交CB于点F. 如图,△ABC的三条角平分线交于点O,过点O作OE⊥BC于点E,求证:∠BOD=∠COE.
如图,△ABC的三条角平分线交于点O,过点O作OE⊥BC于点E,求证:∠BOD=∠COE.