题目内容
已知函数f(x)=m-|3x-4|,且不等式f(x)≥1的解集为{x|1≤x≤
}.
(1)求实数m的值;
(2)若不等式ax+1-f(x)≤0的解集为空集,求实数a的取值范围.
| 5 |
| 3 |
(1)求实数m的值;
(2)若不等式ax+1-f(x)≤0的解集为空集,求实数a的取值范围.
考点:函数恒成立问题
专题:综合题,不等式的解法及应用
分析:(1)不等式f(x)≥1即|3x-4|≤m-1,由其解集为{x|1≤x≤
},得
,解出不等式,根据不等式解集可得关于m的方程;
(2)不等式ax+1-f(x)≤0,即|3x-4|≤1-ax,由不等式ax+1-f(x)≤0的解集为空集,得|3x-4|>1-ax的解集为R,作出函数y=|3x-4|及y=1-ax的图象,则y=1-ax的图象恒在函数y=|3x-4|的下方,由此可得a的不等式.
| 5 |
| 3 |
|
(2)不等式ax+1-f(x)≤0,即|3x-4|≤1-ax,由不等式ax+1-f(x)≤0的解集为空集,得|3x-4|>1-ax的解集为R,作出函数y=|3x-4|及y=1-ax的图象,则y=1-ax的图象恒在函数y=|3x-4|的下方,由此可得a的不等式.
解答:
解:(1)m-|3x-4|≥1⇒|3x-4|≤m-1,
∵不等式f(x)≥1的解集为{x|1≤x≤
},
∴
⇒
⇒
⇒m=2,
∴实数m的值为2;
(2)不等式ax+1-f(x)≤0,即|3x-4|≤1-ax,
∵不等式ax+1-f(x)≤0的解集为空集,
∴|3x-4|>1-ax的解集为R,
作出函数y=|3x-4|及y=1-ax的图象,如图所示:
(2)不等式ax+1-f(x)≤0,即|3x-4|≤1-ax,
∵不等式ax+1-f(x)≤0的解集为空集,
∴|3x-4|>1-ax的解集为R,
作出函数y=|3x-4|及y=1-ax的图象,如图所示:

直线y=1-ax过定点(0,1),当直线y=1-ax与y=-3x+4平行时,-a=-3,
当直线y=1-ax过点(
,0)时,-a=-
,
由图象可知,当|3x-4|>1-ax的解集为R时,-3≤-a<-
,解得
<a≤3,
∴实数a的取值范围是
<a≤3.
∵不等式f(x)≥1的解集为{x|1≤x≤
| 5 |
| 3 |
∴
|
|
|
∴实数m的值为2;
(2)不等式ax+1-f(x)≤0,即|3x-4|≤1-ax,
∵不等式ax+1-f(x)≤0的解集为空集,
∴|3x-4|>1-ax的解集为R,
作出函数y=|3x-4|及y=1-ax的图象,如图所示:
(2)不等式ax+1-f(x)≤0,即|3x-4|≤1-ax,
∵不等式ax+1-f(x)≤0的解集为空集,
∴|3x-4|>1-ax的解集为R,
作出函数y=|3x-4|及y=1-ax的图象,如图所示:

直线y=1-ax过定点(0,1),当直线y=1-ax与y=-3x+4平行时,-a=-3,
当直线y=1-ax过点(
| 4 |
| 3 |
| 3 |
| 4 |
由图象可知,当|3x-4|>1-ax的解集为R时,-3≤-a<-
| 3 |
| 4 |
| 3 |
| 4 |
∴实数a的取值范围是
| 3 |
| 4 |
点评:本题考查绝对值不等式的求解、函数恒成立问题,考查转化思想、数形结合思想,考查学生分析解决问题的能力,属中档题.

练习册系列答案
相关题目
已知两个变量x,y之间具有线性相关关系,试验测得(x,y)的四组值分别为(1,2),(2,4),(3,5),(4,7),则y与x之间的回归直线方程为( )
| A、y=0.8x+3 |
| B、y=-1.2x+7.5 |
| C、y=1.6x+0.5 |
| D、y=1.3x+1.2 |
已知异面直线a、b的方向向量分别为
、
,平面α、β的法向量分别为
、
,则下列命题中是假命题的是( )
| a |
| b |
| m |
| n |
A、对于
| ||||||||||||||
B、若
| ||||||||||||||
C、若cos<
| ||||||||||||||
D、若二面角α-l-β的大小为γ,则γ=<
|
在平面直角坐标系中,O为坐标原点,点A(2,0),将向量
绕点O按逆时针方向旋转
后得向量
,若向量
满足|
-
-
|=1,则|
|的最大值是( )
| OA |
| π |
| 3 |
| OB |
| a |
| a |
| OA |
| OB |
| a |
A、2
| ||||
B、2
| ||||
| C、3 | ||||
D、
|
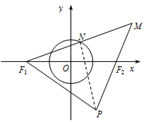 如图,已知定点F1(-2,0),F2(2,0),动点N满足|
如图,已知定点F1(-2,0),F2(2,0),动点N满足|