题目内容
给出下列命题:
①若ab>0,a>b,则
<
;
②若a>|b|,则a2>b2;
③若a>b,c>d,则a-c>b-d;
④若a<b,m>0,则
<
其中真命题的序号是: .
①若ab>0,a>b,则
| 1 |
| a |
| 1 |
| b |
②若a>|b|,则a2>b2;
③若a>b,c>d,则a-c>b-d;
④若a<b,m>0,则
| a |
| b |
| a+m |
| b+m |
其中真命题的序号是:
考点:命题的真假判断与应用
专题:不等式的解法及应用
分析:利用不等式的性质即可得出.
解答:
解:①若ab>0,a>b,则
>
,即
<
,因此正确;
②若a>|b|,利用不等式的性质可得:a2>b2;
③若a>b,c>d,则a-d>b-c,因此③不正确;
④若a<b,m>0,则a(b+m)-b(a+m)=m(a-b)<0,而b(b+m)的正负不正确,因此
<
不一定成立.
综上可知:只有①②是真命题.
故答案为:①②.
| a |
| ab |
| b |
| ab |
| 1 |
| a |
| 1 |
| b |
②若a>|b|,利用不等式的性质可得:a2>b2;
③若a>b,c>d,则a-d>b-c,因此③不正确;
④若a<b,m>0,则a(b+m)-b(a+m)=m(a-b)<0,而b(b+m)的正负不正确,因此
| a |
| b |
| a+m |
| b+m |
综上可知:只有①②是真命题.
故答案为:①②.
点评:本题考查了不等式的性质,属于基础题.

练习册系列答案
相关题目
已知两个变量x,y之间具有线性相关关系,试验测得(x,y)的四组值分别为(1,2),(2,4),(3,5),(4,7),则y与x之间的回归直线方程为( )
| A、y=0.8x+3 |
| B、y=-1.2x+7.5 |
| C、y=1.6x+0.5 |
| D、y=1.3x+1.2 |
已知f(x)=
定义域为M,g(x)=ex值域为N,则M∩N=( )
| 1-x |
| A、[0,1] |
| B、(0,1] |
| C、(0,+∞) |
| D、[1,+∞) |
焦点在y轴上的双曲线的一条渐近线方程是x-
y=0,此双曲线的离心率为( )
| 3 |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
在平面直角坐标系中,O为坐标原点,点A(2,0),将向量
绕点O按逆时针方向旋转
后得向量
,若向量
满足|
-
-
|=1,则|
|的最大值是( )
| OA |
| π |
| 3 |
| OB |
| a |
| a |
| OA |
| OB |
| a |
A、2
| ||||
B、2
| ||||
| C、3 | ||||
D、
|
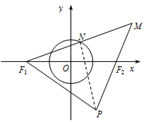 如图,已知定点F1(-2,0),F2(2,0),动点N满足|
如图,已知定点F1(-2,0),F2(2,0),动点N满足|