题目内容
9.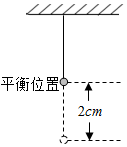 如图所示,一个小球做简谐运动,当时间t=0s时,小球在平衡位置,当t=1s时,小球第一次达到偏离平衡位置最大距离,这时小球离开平衡位置2cm,若该简谐运动的解析式为y=Asin(ωt+φ),则A,ω,φ的值分别是多少?
如图所示,一个小球做简谐运动,当时间t=0s时,小球在平衡位置,当t=1s时,小球第一次达到偏离平衡位置最大距离,这时小球离开平衡位置2cm,若该简谐运动的解析式为y=Asin(ωt+φ),则A,ω,φ的值分别是多少?
分析 根据简谐运动y=Asin(ωt+φ)的物理意义,可分别求出A,ω,φ的值.
解答 解:t=0s,小球在平衡位置,φ=0,
由$\frac{T}{4}$=1s,T=4s,$ω=\frac{2π}{T}$=$\frac{π}{2}$,
∴A=2cm,
∴y=2sin$\frac{π}{2}$t.
点评 本题考查y=Asin(ωt+φ)函数图象的物理意义,属于基础题.

练习册系列答案
相关题目
19.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1、F2,点P在双曲线的右支上,且|PF1|=4|PF2|,则此双曲线的离心率e的最大值为( )
| A. | $\frac{5}{4}$ | B. | $\frac{6}{5}$ | C. | $\frac{5}{3}$ | D. | $\frac{8}{5}$ |
17.双曲线E:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的右焦点为F(c,0),若圆C:(x-c)2+y2=4a2与双曲线E的渐近线相切,则E的离心率为( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{3}+1}{2}$ | C. | $\sqrt{5}$ | D. | $\sqrt{3}$ |
4.双曲线$\frac{x^2}{4}-\frac{y^2}{5}=1$的焦距等于( )
| A. | 2 | B. | 4 | C. | 3 | D. | 6 |
14.过点E(1,0)作两条互相垂直的直线交抛物线y2=4x于点A、B、C、D,且M、N分别是AB、CD的中点,则三角形EMN面积的最小值为( )
| A. | 2 | B. | 3 | C. | $\frac{1}{3}$ | D. | 4 |
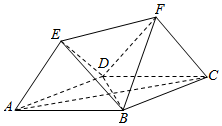 如图,多面体ABCDEF中,四边形ABCD为菱形,且∠DAB=60°,EF∥AC,AD=2,EA=ED=EF=$\sqrt{3}$.
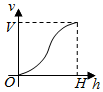
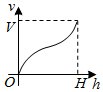
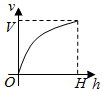
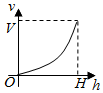
如图,多面体ABCDEF中,四边形ABCD为菱形,且∠DAB=60°,EF∥AC,AD=2,EA=ED=EF=$\sqrt{3}$.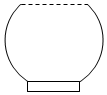 一个高为H容积为V的鱼缸的轴截面如图所示.现向空鱼缸内注水,直到注满为止.当鱼缸水深为h时,水的体积记为v.函数v=f(h)的大致图象可能是( )
一个高为H容积为V的鱼缸的轴截面如图所示.现向空鱼缸内注水,直到注满为止.当鱼缸水深为h时,水的体积记为v.函数v=f(h)的大致图象可能是( )