题目内容
1.过抛物线的顶点任作互相垂直的两条弦,交抛物线于两点,求证:这两点所连线段中点的轨迹是抛物线.分析 先设A(x1,y1)、B(x2,y2)及中点P的坐标,根据中点的定义得到三点坐标之间的关系,再由OA⊥OB得到1x2+y1y2=0,结合A、B两点在抛物线上满足抛物线方程可得到y1y2、y12+y22的关系消去x1、y1、x2、y2可得到最后答案.
解答 证明:不妨设抛物线y2=2px(p>0),设A、B两点坐标为(x1,y1)、(x2,y2),AB中点P坐标为(x0,y0),则x1+x2=2x0,y1+y2=2y0
由OA⊥OB得x1x2+y1y2=0.
∴(y1y2)2=4p2x1x2=-4p2y1y2
∴y1y2=-4p2
∵y12+y22=2p(x1+x2)
∴(y1+y2)2-2y1y2=2p(x1+x2)
∴4y02+8p2=4px0
即y02=px0-2p2
∴中点轨迹方程为:y2=px-2p2,
∴这两点所连线段中点的轨迹是抛物线.
点评 本题主要考查直线和抛物线的综合问题,考查轨迹方程,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
11.已知F1,F2是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,若点F2关于直线y=$\frac{b}{a}$x的对称点M也在双曲线上,则该双曲线的离心率为( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{5}$ | D. | 2 |
12.用更相减损术求得81与135的最大公约数是( )
| A. | 54 | B. | 27 | C. | 9 | D. | 81 |
11.用秦九韶算法求函数f(x)=3x5-2x4+2x3-4x2-7当x=2的值时,v3的结果是( )
| A. | 4 | B. | 10 | C. | 16 | D. | 33 |
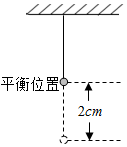 如图所示,一个小球做简谐运动,当时间t=0s时,小球在平衡位置,当t=1s时,小球第一次达到偏离平衡位置最大距离,这时小球离开平衡位置2cm,若该简谐运动的解析式为y=Asin(ωt+φ),则A,ω,φ的值分别是多少?
如图所示,一个小球做简谐运动,当时间t=0s时,小球在平衡位置,当t=1s时,小球第一次达到偏离平衡位置最大距离,这时小球离开平衡位置2cm,若该简谐运动的解析式为y=Asin(ωt+φ),则A,ω,φ的值分别是多少?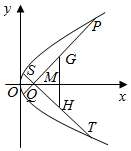 已知抛物线C:y2=2px(p>0)的焦点是F,点D(1,y0)是抛物线C上的点,且|DF|=3.
已知抛物线C:y2=2px(p>0)的焦点是F,点D(1,y0)是抛物线C上的点,且|DF|=3.