题目内容
14.过点E(1,0)作两条互相垂直的直线交抛物线y2=4x于点A、B、C、D,且M、N分别是AB、CD的中点,则三角形EMN面积的最小值为( )| A. | 2 | B. | 3 | C. | $\frac{1}{3}$ | D. | 4 |
分析 不妨设AB的斜率k1=k>0,求出CD的斜率k2=-$\frac{1}{k}$<0,利用点斜式方程求出直线AB、CD的方程,与抛物线方程联立消x得关于y的一元二次方程,根据韦达定理即可求得中点M、N的坐标,利用点斜式方程求出直线MN的方程,再求出直线MN与x轴的交点坐标,可得△EMN的面积,利用基本不等式求△EMN面积的最小值.
解答 解:由题意不妨设AB的斜率k1=k>0,则CD的斜率k2=-$\frac{1}{k}$<0,
所以AB的直线方程是:y=k(x-1),CD的直线方程是y=-$\frac{1}{k}$(x-1),
设A(x1,y1),B(x2,y2),
由$\left\{\begin{array}{l}{y=k(x-1)}\\{{y}^{2}=4x}\end{array}\right.$得,k2x2-(2k2+4)x+k2=0,
则x1+x2=2+$\frac{4}{{k}^{2}}$,x1x2=1,
所以y1+y2=k(x1-1)+k(x2-1)=k(2+$\frac{4}{{k}^{2}}$)-2k=$\frac{4}{k}$,
因为M是AB的中点,所以点M(1+$\frac{2}{{k}^{2}}$,$\frac{2}{k}$),
同理可得,点N(1+2k2,-2k),
所以直线MN的方程是:y+2k=$\frac{\frac{1}{k}+k}{\frac{1}{{k}^{2}}-{k}^{2}}$(x-1-2k2),令y=0,得x=3,
则直线MN与x轴的交点是(3,0),
所以△EMN面积S=$\frac{1}{2}$(3-1)($\frac{2}{k}$+2k)=$\frac{2}{k}$+2k≥2$\sqrt{\frac{2}{k}×2k}$=4,
当且仅当$\frac{2}{k}$=2k时取等号,此时k=1,
所以△EMN面积的最小值是4.
故选:D.
点评 本题主要考查抛物线的几何性质,直线方程的求解,以及直线与抛物线的位置关系等基础知识,同时考查解析几何的基本思想方法和运算求解能力.

| A. | $\sqrt{6}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{3}$ |
| A. | x1+x2+x3>0 | B. | x1+x2+x3<0 | C. | f(x1+x2+x3)≥0 | D. | f(x1+x2+x3)≤0 |
| 男性 | 女性 | 合计 | |
| 无酒驾习惯 | 31 | ||
| 有酒驾习惯 | 8 | ||
| 合计 | 89 |
(1)将如表中空白部分数据补充完整;
(2)若从有酒驾习惯的人中按性别用分层抽样的方法抽取8人参加某项活动,现从这8人中随机抽取2人,记抽到女性的人数为X,求X得分布列和数学期望.
| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{2}$ |
| A. | 经过圆外一点与圆相切的直线至多有两条 | |
| B. | 经过圆外一点与圆相切的直线有两条 | |
| C. | 经过圆外一点与圆相切的直线不存在 | |
| D. | 经过圆外一点与圆相切的直线至多有一条 |
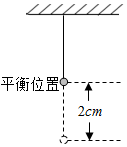 如图所示,一个小球做简谐运动,当时间t=0s时,小球在平衡位置,当t=1s时,小球第一次达到偏离平衡位置最大距离,这时小球离开平衡位置2cm,若该简谐运动的解析式为y=Asin(ωt+φ),则A,ω,φ的值分别是多少?
如图所示,一个小球做简谐运动,当时间t=0s时,小球在平衡位置,当t=1s时,小球第一次达到偏离平衡位置最大距离,这时小球离开平衡位置2cm,若该简谐运动的解析式为y=Asin(ωt+φ),则A,ω,φ的值分别是多少?