题目内容
18.从5名女同学和4名男同学中选出4人参加四场不同的演讲,分别按下列要求,各有多少种不同选法?(1)男、女同学各2名;
(2)男、女同学分别至少有1名;
(3)男、女同学分别至少有1名且男同学甲与女同学乙不能同时选出.
分析 (1)可分两步求解,先选出四人,再作一全排列计算出不同的选法种数;
(2)可分两步求解,先选出四人,再作一全排列计算出不同的选法种数,由于“男、女同学分别至少有1名”包括了三个事件,“一男三女”,“二男二女”,“三男一女”,选人时要分三类计数,然后再进行全排列;
(3)可计算出男同学甲与女同学乙同时选出的情况种数,从(2)的结果中排除掉,即可得到事件“在(2)的前提下,男同学甲与女同学乙不能同时选出”的选法种数
解答 解:(1)男、女同学各2名的选法有C42×C52=6×10=60种,故总的不同选法有60×A44=1440种;
即男女同学各两名的选法共有1440种.
(2)“男、女同学分别至少有1名”包括有“一男三女”,“二男二女”,“三男一女”,故选人种数为C41×C53+C42×C52+C43×C51=40+60+20=120
故总的安排方法有120×A44=2880
故不同的选法有2880种.
(3)可计算男同学甲与女同学乙同时选出的种数,由于已有两人,故再选两人即可,此两人可能是两男,一男一女,两女,故总的选法有C32+C41×C31+C42=21
故总的选法有2880-21×A44=2376
故不同的选法种数是2376种
点评 本题考查排列、组合及简单计数问题,解题的关键是正确理解题设中的事件,及理解计数原理,本题考查了分类的及运算的能力.

练习册系列答案
相关题目
8.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的右焦点为F,以F为圆心和双曲线的渐近线相切的圆与双曲线的一个交点为M,且MF与双曲线的实轴垂直,则双曲线C的离心率为( )
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\sqrt{5}$ | C. | $\sqrt{2}$ | D. | 2 |
3.命题“经过圆外一点与圆相切的直线至少有一条”的否定是( )
| A. | 经过圆外一点与圆相切的直线至多有两条 | |
| B. | 经过圆外一点与圆相切的直线有两条 | |
| C. | 经过圆外一点与圆相切的直线不存在 | |
| D. | 经过圆外一点与圆相切的直线至多有一条 |
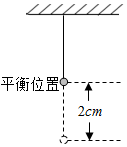 如图所示,一个小球做简谐运动,当时间t=0s时,小球在平衡位置,当t=1s时,小球第一次达到偏离平衡位置最大距离,这时小球离开平衡位置2cm,若该简谐运动的解析式为y=Asin(ωt+φ),则A,ω,φ的值分别是多少?
如图所示,一个小球做简谐运动,当时间t=0s时,小球在平衡位置,当t=1s时,小球第一次达到偏离平衡位置最大距离,这时小球离开平衡位置2cm,若该简谐运动的解析式为y=Asin(ωt+φ),则A,ω,φ的值分别是多少?