题目内容
将n2个正整数1、2、3、…、n2(n≥2)任意排成n行n列的数表.对于某一个数表,计算某行或某列中的任意两个数a、b(a>b)的比值
,称这些比值中的最小值为这个数表的“特征值”.当n=2时,数表的所有可能的“特征值”的最大值为( )
| a |
| b |
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
考点:归纳推理
专题:简易逻辑
分析:可设1在第一行第一列,考虑与1同行或同列的两个数的可能,可得特征值,比较后可得答案.
解答:
解:当n=2时,这4个数分别为1、2、3、4,排成了两行两列的数表,
当1、2同行或同列时,这个数表的“特征值”为
;
当1、3同行或同列时,这个数表的特征值分别为
或
;
当1、4同行或同列时,这个数表的“特征值”为
或
,
故这些可能的“特征值”的最大值为
.
故选:B.
当1、2同行或同列时,这个数表的“特征值”为
| 4 |
| 3 |
当1、3同行或同列时,这个数表的特征值分别为
| 4 |
| 3 |
| 3 |
| 2 |
当1、4同行或同列时,这个数表的“特征值”为
| 4 |
| 3 |
| 3 |
| 2 |
故这些可能的“特征值”的最大值为
| 3 |
| 2 |
故选:B.
点评:题考查类比推理和归纳推理,属基础题.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
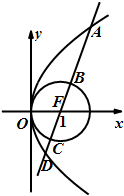 已知抛物线y2=4x,圆F:(x-1)2+y2=1,过点F作直线l,自上而下顺次与上述两曲线交于点A,B,C,D(如图所示),则|AB|•|CD|的值正确的是( )
已知抛物线y2=4x,圆F:(x-1)2+y2=1,过点F作直线l,自上而下顺次与上述两曲线交于点A,B,C,D(如图所示),则|AB|•|CD|的值正确的是( )| A、等于1 | B、最小值是1 |
| C、等于4 | D、最大值是4 |
已知函数f(x)=
若直线y=m与函数f(x)的图象有两个不同的交点,则实数m的取值范围是( )
|
| A、m∈R | B、m>1 |
| C、m>0 | D、0<m<1 |
已知函数f(x)满足f(x+1)=
+f(x)(x∈R),且f(1)=
,则数列{f(n)}(n∈N*)前20项的和为( )
| 3 |
| 2 |
| 5 |
| 2 |
| A、305 | B、315 |
| C、325 | D、335 |
双曲线
-
=1的离心率的值为( )
| y2 |
| 4 |
| x2 |
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数y=sin(-2x+
)在区间[0,π]上的单调递增区间为( )
| π |
| 3 |
A、[
| ||||
B、[0,
| ||||
C、[
| ||||
D、[
|
已知函数f(x)=ex-2x+a有零点,则实数a的取值范围是( )
| A、(-∞,2ln2-2] |
| B、[2ln2-2,+∞) |
| C、[2ln2,+∞) |
| D、[2ln2-2,2ln2] |
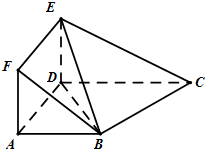 如图所示,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,
如图所示,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,