题目内容
双曲线
-
=1的离心率的值为（ ）
| y2 |
| 4 |
| x2 |
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：双曲线
-
=1中a=2，c=3，利用离心率公式，可得结论．
| y2 |
| 4 |
| x2 |
| 5 |
解答：
解：双曲线
-
=1中a=2，c=3，
∴离心率e=
=
故选：C．
| y2 |
| 4 |
| x2 |
| 5 |
∴离心率e=
| c |
| a |
| 3 |
| 2 |
故选：C．
点评：本题考查双曲线的方程与性质，考查学生的计算能力，属于基础题．
练习册系列答案
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
相关题目
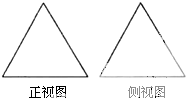如图是两个全等的正三角形，给定下列三个命题：①存在四棱锥，其正视图、侧视图如图；②存在三棱锥，其正视图、侧视图如图；③存在圆锥，其正视图、侧视图如图．其中真命题的个数是（ ）| A、3 | B、2 | C、1 | D、0 |
对于定义域为D的函数y=f（x）和常数C，若对任意正实数ξ，存在x∈D，使得0＜|f（x）-c|＜ξ恒成立，则称函数y=f（x）为“敛C函数”．现给出如下函数：
①f（x）=x（x∈Z）； ②f（x）=（
）x+1（x∈Z）；③f（x）=log2x；
其中为“敛1函数”的有（ ）
①f（x）=x（x∈Z）； ②f（x）=（
| 1 |
| 2 |
其中为“敛1函数”的有（ ）
| A、② | B、①③ | C、②③ | D、①③ |
将n2个正整数1、2、3、…、n2（n≥2）任意排成n行n列的数表．对于某一个数表，计算某行或某列中的任意两个数a、b（a＞b）的比值
，称这些比值中的最小值为这个数表的“特征值”．当n=2时，数表的所有可能的“特征值”的最大值为（ ）
| a |
| b |
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
若实数x，y满足条件
，则x-2y的最小值是（ ）
|
| A、-3 | B、-2 | C、-1 | D、0 |
设全集U=R，A={x∈N|y=ln（2-x）}，B={x|2x（x-2）≤1}，A∩B=（ ）
| A、{x|x≥1} |
| B、{x|1≤x＜2} |
| C、{1} |
| D、{0，1} |
已知如图为函数f（x）=2sin（ωx+φ）（ω＞0，0＜φ＜