题目内容
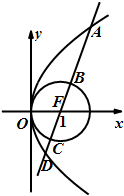 已知抛物线y2=4x,圆F:(x-1)2+y2=1,过点F作直线l,自上而下顺次与上述两曲线交于点A,B,C,D(如图所示),则|AB|•|CD|的值正确的是( )
已知抛物线y2=4x,圆F:(x-1)2+y2=1,过点F作直线l,自上而下顺次与上述两曲线交于点A,B,C,D(如图所示),则|AB|•|CD|的值正确的是( )| A、等于1 | B、最小值是1 |
| C、等于4 | D、最大值是4 |
考点:抛物线的简单性质,直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程
分析:利用抛物线的定义和|AF|=|AB|+1就可得出|AB|=xA,同理可得:|CD|=xD,要分l⊥x轴和l不垂直x轴两种情况分别求值,当l⊥x轴时易求,当l不垂直x轴时,将直线的方程代入抛物线方程,利用根与系数关系可求得.
解答:
解:∵y2=4x,焦点F(1,0),准线 l0:x=-1.
由定义得:|AF|=xA+1,
又∵|AF|=|AB|+1,∴|AB|=xA,
同理:|CD|=xD,
当l⊥x轴时,则xD=xA=1,∴|AB|•|CD|=1
当l:y=k(x-1)时,代入抛物线方程,得:k2x2-(2k2+4)x+k2=0,
∴xAxD=1,∴|AB|•|CD|=1
综上所述,|AB|•|CD|=1,
故选:A.

由定义得:|AF|=xA+1,
又∵|AF|=|AB|+1,∴|AB|=xA,
同理:|CD|=xD,
当l⊥x轴时,则xD=xA=1,∴|AB|•|CD|=1
当l:y=k(x-1)时,代入抛物线方程,得:k2x2-(2k2+4)x+k2=0,
∴xAxD=1,∴|AB|•|CD|=1
综上所述,|AB|•|CD|=1,
故选:A.
点评:本题主要考查抛物线的定义、一元二次方程的根与系数关系,考查学生的计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设定义在(0,
)上的函数y=2sinx的图象分别与y=cosx,y=tanx的图象交于点(x1,y1),(x2,y2),则
y1+y2=( )
| π |
| 2 |
| 5 |
A、3+
| ||
B、2+
| ||
C、3+
| ||
D、2+
|
已知斜率为k=1的直线与双曲线
-
=1(a>0,b>0)交于A、B两点,若A、B的中点为M(1,3),则双曲线的渐近线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、x±
| ||
B、
| ||
| C、x±2y=0 | ||
| D、2x±y=0 |
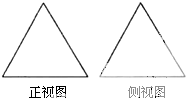 如图是两个全等的正三角形,给定下列三个命题:①存在四棱锥,其正视图、侧视图如图;②存在三棱锥,其正视图、侧视图如图;③存在圆锥,其正视图、侧视图如图.其中真命题的个数是( )
如图是两个全等的正三角形,给定下列三个命题:①存在四棱锥,其正视图、侧视图如图;②存在三棱锥,其正视图、侧视图如图;③存在圆锥,其正视图、侧视图如图.其中真命题的个数是( )| A、3 | B、2 | C、1 | D、0 |
已知i为虚数单位,则复数
等于( )
| (2+i)(1-i)2 |
| 1-2i |
| A、2 | B、-2 | C、2i | D、-2i |
将n2个正整数1、2、3、…、n2(n≥2)任意排成n行n列的数表.对于某一个数表,计算某行或某列中的任意两个数a、b(a>b)的比值
,称这些比值中的最小值为这个数表的“特征值”.当n=2时,数表的所有可能的“特征值”的最大值为( )
| a |
| b |
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
如图所示的流程图,若输入x的值为2,则输出x的值为( )


| A、5 | B、7 | C、125 | D、127 |