题目内容
已知函数f（x）满足f（x+1）=
+f（x）（x∈R），且f（1）=
，则数列{f（n）}（n∈N*）前20项的和为（ ）
| 3 |
| 2 |
| 5 |
| 2 |
| A、305 | B、315 |
| C、325 | D、335 |
考点：数列的求和
专题：等差数列与等比数列
分析：由已知条件推导出{f（n）}是以
为首项，
为公差的等差数列，由此能求出数列{f（n）}（n∈N*）前20项的和．
| 5 |
| 2 |
| 3 |
| 2 |
解答：
解：∵函数f（x）满足f（x+1）=
+f（x）（x∈R），
且f（1）=
，
∴f（2）=
+
，
f（3）=
+
+
，…，f（n）=
+f（n-1），
∴{f（n）}是以
为首项，
为公差的等差数列．
∴数列{f（n）}（n∈N*）前20项的和S20=20×
+
×
=335．
故选：D．
| 3 |
| 2 |
且f（1）=
| 5 |
| 2 |
∴f（2）=
| 3 |
| 2 |
| 5 |
| 2 |
f（3）=
| 3 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
| 3 |
| 2 |
∴{f（n）}是以
| 5 |
| 2 |
| 3 |
| 2 |
∴数列{f（n）}（n∈N*）前20项的和S20=20×
| 5 |
| 2 |
| 20(20-1) |
| 2 |
| 3 |
| 2 |
故选：D．
点评：本题考查数列的前20项和的求法，是中档题，解题时要认真审题，注意递推思想的合理运用．
练习册系列答案
相关题目
已知斜率为k=1的直线与双曲线
-
=1（a＞0，b＞0）交于A、B两点，若A、B的中点为M（1，3），则双曲线的渐近线方程为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、x±
| ||
B、
| ||
| C、x±2y=0 | ||
| D、2x±y=0 |
已知i为虚数单位，则复数
等于（ ）
| (2+i)(1-i)2 |
| 1-2i |
| A、2 | B、-2 | C、2i | D、-2i |
已知函数f（x）=（x-a）（x-b）+2，（a＜b），若α，β（α＜β）是方程f（x）=0的两个根，则实数a，b，α，β之间的大小关系是（ ）
| A、α＜a＜b＜β |
| B、a＜α＜β＜b |
| C、α＜b＜a＜β |
| D、α＜a＜β＜b |
将n2个正整数1、2、3、…、n2（n≥2）任意排成n行n列的数表．对于某一个数表，计算某行或某列中的任意两个数a、b（a＞b）的比值
，称这些比值中的最小值为这个数表的“特征值”．当n=2时，数表的所有可能的“特征值”的最大值为（ ）
| a |
| b |
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
执行如图所示的程序框图，则输出的结果为（ ）
| A、20 | B、30 | C、40 | D、50 |
已知F1，F2为双曲线
-
=1（a＞0，b＞0）的左右焦点，M为此双曲线上的一点，满足|MF1|=3|MF2|，那么此双曲线的离心率的取值范围是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| A、（1，2） |
| B、（1，2] |
| C、（0，2） |
| D、[2，+∞） |
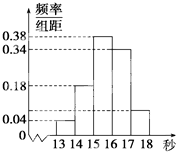为调查某市学生百米运动成绩，从该市学生中按照男女生比例随机抽取50名学生进行百米测试，测试成绩全部都介于13秒到18秒之间，将测试结果按如下方式分成五组，第一组[13，14），第二组[14，15），…，第五组[17，18]，如图是按上述分组方法得到的频率分布直方图．