题目内容
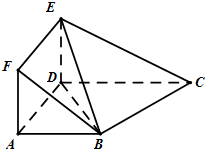 如图所示,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,
如图所示,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,CD=2AB=2AD.
(Ⅰ)求证:BC⊥BE;
(Ⅱ)求直线CE与平面BDE所成角的正切值;
(Ⅲ)在EC上找一点M,使得BM∥平面ADEF,请确定M点的位置,并给出证明.
考点:直线与平面平行的性质,直线与平面所成的角
专题:证明题,空间位置关系与距离
分析:(I)根据面面垂直的性质可证DE⊥平面ABCD,利用勾股定理证明BC⊥BE;
(II)根据直线与平面所成角的定义证明∠CEB为CE与面BDE所成的角,在Rt△BCE中,求tan∠CEB的值;
(III)取EC中点M,利用面面平行证明BM∥面ADEF.
(II)根据直线与平面所成角的定义证明∠CEB为CE与面BDE所成的角,在Rt△BCE中,求tan∠CEB的值;
(III)取EC中点M,利用面面平行证明BM∥面ADEF.
解答:
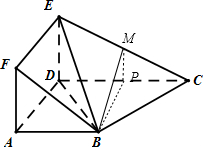 解:(I)由已知:平面ADEF⊥平面ABCD,平面ADEF∩平面ABCD=AD.
解:(I)由已知:平面ADEF⊥平面ABCD,平面ADEF∩平面ABCD=AD.
DE⊥AD,DE?PMADEF,∴DE⊥平面ABCD,∴DE⊥BC,
设CD=2AB=2AD=2,∴DE=1,则BC=
,BD=
,BE=
,CE=
,
∴CE2=BE2+BC2,∴BC⊥BE;
(II)由(1)可知:BC⊥BE,由BC⊥DE,∴BC⊥平面BDE,
∴∠CEB为CE与面BDE所成的角.
在Rt△BCE中,tan∠CEB=
=
=
,
(III)取EC中点M,则BM∥面ADEF,
证明如下:取CD的中点P,连结MB、MP,则BP∥AD,∴BP∥面ADEF,
又M、P分别为EC、DC的中点,∴MP∥ED,∴MP∥面ADEF,又BP∩MP=P,∴面BMP∥面ADEF,
BM?平面BMP,∴BM∥面ADEF.
 解:(I)由已知:平面ADEF⊥平面ABCD,平面ADEF∩平面ABCD=AD.
解:(I)由已知:平面ADEF⊥平面ABCD,平面ADEF∩平面ABCD=AD.DE⊥AD,DE?PMADEF,∴DE⊥平面ABCD,∴DE⊥BC,
设CD=2AB=2AD=2,∴DE=1,则BC=
| 2 |
| 2 |
| 3 |
| 5 |
∴CE2=BE2+BC2,∴BC⊥BE;
(II)由(1)可知:BC⊥BE,由BC⊥DE,∴BC⊥平面BDE,
∴∠CEB为CE与面BDE所成的角.
在Rt△BCE中,tan∠CEB=
| BC |
| BE |
| ||
|
| ||
| 3 |
(III)取EC中点M,则BM∥面ADEF,
证明如下:取CD的中点P,连结MB、MP,则BP∥AD,∴BP∥面ADEF,
又M、P分别为EC、DC的中点,∴MP∥ED,∴MP∥面ADEF,又BP∩MP=P,∴面BMP∥面ADEF,
BM?平面BMP,∴BM∥面ADEF.
点评:本题考查了面面平行、面面垂直的性质及直线与平面所成角的求法,考查了学生的空间想象能力与推理论证能力,综合性强.

练习册系列答案
相关题目
将n2个正整数1、2、3、…、n2(n≥2)任意排成n行n列的数表.对于某一个数表,计算某行或某列中的任意两个数a、b(a>b)的比值
,称这些比值中的最小值为这个数表的“特征值”.当n=2时,数表的所有可能的“特征值”的最大值为( )
| a |
| b |
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
如图所示的流程图,若输入x的值为2,则输出x的值为( )


| A、5 | B、7 | C、125 | D、127 |


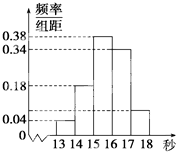 为调查某市学生百米运动成绩,从该市学生中按照男女生比例随机抽取50名学生进行百米测试,测试成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.
为调查某市学生百米运动成绩,从该市学生中按照男女生比例随机抽取50名学生进行百米测试,测试成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图. 已知如图为函数f(x)=2sin(ωx+φ)(ω>0,0<φ<
已知如图为函数f(x)=2sin(ωx+φ)(ω>0,0<φ<