题目内容
关于x的方程(x2-1)2-|x2-1|+k=0恰有8个不同的实根,则k的取值范围是 .
考点:根的存在性及根的个数判断,函数的图象与图象变化
专题:函数的性质及应用
分析:将方程根的问题转化成函数图象的问题,画出函数图象,结合图象可得结论.
解答:
 解:关于x的方程(x2-1)2-|x2-1|+k
解:关于x的方程(x2-1)2-|x2-1|+k
=0,
可化为(x2-1)2-(x2-1)+k=0,
(x≥1或x≤-1)…(1)
或(x2-1)2+(x2-1)+k=0,
(-1<x<1)…(2)
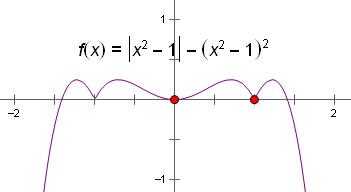
令f(x)=|x2-1|-(x2-1)2,
则由题意可得,函数f(x)的图象和
直线y=k有8个交点.
令t=x2-1≥0,则f(x)=|t|-t2=g(t),显然函数g(t)关于变量t是偶函数,
当t=±
时,f(x)=g(t)取得最大值为
,此时对应的x值有4个:±
、±
.
显然,当函数f(x)的图象和直线y=k有8个交点时,0<k<
,
故答案为:(0,
).
 解:关于x的方程(x2-1)2-|x2-1|+k
解:关于x的方程(x2-1)2-|x2-1|+k=0,
可化为(x2-1)2-(x2-1)+k=0,
(x≥1或x≤-1)…(1)
或(x2-1)2+(x2-1)+k=0,
(-1<x<1)…(2)
令f(x)=|x2-1|-(x2-1)2,
则由题意可得,函数f(x)的图象和
直线y=k有8个交点.
令t=x2-1≥0,则f(x)=|t|-t2=g(t),显然函数g(t)关于变量t是偶函数,
当t=±
| 1 |
| 2 |
| 1 |
| 4 |
| ||
| 2 |
| ||
| 2 |
显然,当函数f(x)的图象和直线y=k有8个交点时,0<k<
| 1 |
| 4 |
故答案为:(0,
| 1 |
| 4 |
点评:本题主要考查了分段函数,以及函数与方程的思想,数形结合的思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
(文)Sn=1-2+3-4+5-6+…+(-1)n+1•n,则S100+S200+S301等于( )
| A、1 | B、-1 | C、51 | D、52 |
若ABCD为正方形,E是CD的中点,则
=
,
=
,则
=( )
| AB |
| a |
| AD |
| b |
| AE |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
若函数f(x)=x2+a|x-1|(a∈R),则对不同的实数a,函数f(x)的单调区间的个数有可能的是( )
| A、1个或2个 |
| B、2个或3个 |
| C、3个或4个 |
| D、2个或4个 |
若圆(x-1)2+(y-2)2=5的圆心到直线x-y+a=0的距离为
,则a的值为( )
| ||
| 2 |
| A、-2或2 | ||
B、
| ||
| C、2或0 | ||
| D、-2或0 |
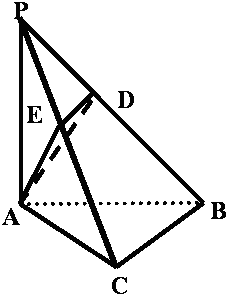 如图,在三梭锥P-ABC中,PA⊥底面ABC,PA=AB=2,∠ABC=60°,∠BCA=90°,点D、E分别在棱PB、PC上,且DE∥BC
如图,在三梭锥P-ABC中,PA⊥底面ABC,PA=AB=2,∠ABC=60°,∠BCA=90°,点D、E分别在棱PB、PC上,且DE∥BC