Question

已知在边长为1的正方形ABCD的一边上取一点E，使AE=

1

4

AD，过AB的中点F作HF⊥EC于H．
（1）求证：FH=FA；
（2）求EH：HC的值．

Answer 1

考点：平行线分线段成比例定理

专题：立体几何

分析：如图所示．建立直角坐标系．可得A（0，0），C（1，1），E(0，

1

4

)，F(

1

2

，0)．利用相互垂直的直线斜率之间的关系可得直线FH的斜率，再利用点斜式分别得到直线CE、FH的方程，即可得到点H的坐标，利用两点间的距离公式即可得出答案．

解答： 解：如图所示．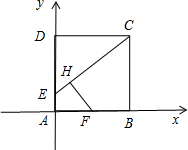
建立直角坐标系．
则A（0，0），C（1，1），E(0，

1

4

)，F(

1

2

，0)．
直线CE：y=

1- 1 4

1-0

x+

1

4

，化为y=

3

4

x+

1

4

．
∵FH⊥CE，∴kFH=-

4

3

．
∴直线FH：y=-

4

3

(x-

1

2

)，即y=-

4

3

x+

2

3

．
联立

y= 3 4 x+ 1 4 y=- 4 3 x+ 2 3

，
解得

x= 1 5 y= 2 5

，即H(

1

5

，

2

5

)．
∴|FH|=

( 1 2 - 1 5 )2+( 2 5 )2

=

1

2

，
∵|AF|=

1

2

，
∴|FH|=|AF|．
又∵|EH|=

( 1 5 )2+( 1 4 - 2 5 )2

=

1

4

，|CH|=

(1- 1 5 )2+(1- 2 5 )2

=1．
∴EH：HC=1：4．

点评：本题考查了通过建立直角坐标系证明几何问题、相互垂直的直线斜率之间的关系、点斜式、两点间的距离公式，属于中档题．