题目内容
若函数f（x）=x2+a|x-1|（a∈R），则对不同的实数a，函数f（x）的单调区间的个数有可能的是（ ）
| A、1个或2个 |
| B、2个或3个 |
| C、3个或4个 |
| D、2个或4个 |
考点：函数单调性的判断与证明
专题：函数的性质及应用
分析：先令a=0，再将函数化为分段函数，利用分类讨论的方法，通过出画函数图象判断f（x）的单调区间的个数，从而得出正确判断．
解答：
解：当a=0时，f（x）=x2，是一元二次函数，在R上有两个单调区间；
当a≠0时，∵f（x）=x2+a|x-1|，
∴f（x）=
；
∴f（x）是以x=1为分界线的两段抛物线，当-
＞1，即a＜-2，得
＜-1；
画出函数图象如图，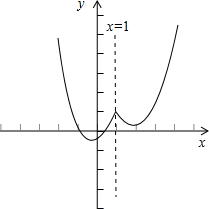
，
此时函数f（x）有四个单调区间；
故选：D．
当a≠0时，∵f（x）=x2+a|x-1|，
∴f（x）=
|
∴f（x）是以x=1为分界线的两段抛物线，当-
| a |
| 2 |
| a |
| 2 |
画出函数图象如图，
，此时函数f（x）有四个单调区间；
故选：D．
点评：本题考查了含绝对值函数的单调区间的判断问题，利用分类讨论思想，结合函数图象，可以得出结论．
练习册系列答案
相关题目
若k的值使得过A（1，1）可以做两条直线与圆x2+y2+kx-2y-
k=0相切，则k的取值范围是（ ）
| 5 |
| 4 |
| A、k＜0 |
| B、k＜-4或-1＜k＜0 |
| C、k＜-4 |
| D、k＜-4或k＞-1 |
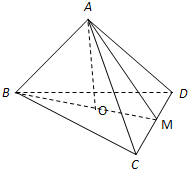已知正四面体ABCD的棱长为a，点O是△BCD的中心，点M是CD中点．