题目内容
已知实数x,y满足
,则 z=
的最大值为 .
|
| (y+x)(y-x) |
| xy |
考点:简单线性规划的应用
专题:数形结合法,不等式的解法及应用
分析:作出满足
的可行域,可得
的范围,化简目标函数,利用其单调性,可求最大值.
|
| y |
| x |
解答:
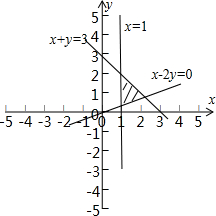 解:满足
解:满足
的可行域如图所示,三个顶点的坐标分别为(1,
),(1,2),(2,1),
∴
的值分别为
,2,
令
=t,则t∈[
,2]
∴z=
=
=
-
=t-
∴该函数在[
,2]上单调递增,
∴t=2时,z=
的最大值为
.
故答案为:
.
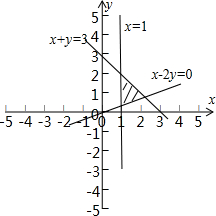 解:满足
解:满足
|
| 1 |
| 2 |
∴
| y |
| x |
| 1 |
| 2 |
令
| y |
| x |
| 1 |
| 2 |
∴z=
| (y+x)(y-x) |
| xy |
| y2-x2 |
| xy |
| y |
| x |
| x |
| y |
| 1 |
| t |
∴该函数在[
| 1 |
| 2 |
∴t=2时,z=
| (y+x)(y-x) |
| xy |
| 3 |
| 2 |
故答案为:
| 3 |
| 2 |
点评:本题考查线性规划知识的运用,考查函数的单调性,确定可行域是关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
一个半径为R的扇形,周长为4R,则这个扇形的面积是( )
| A、2R2 | ||
| B、2 | ||
C、
| ||
| D、R2 |