题目内容
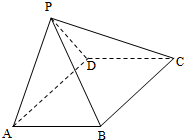 如图,四棱锥P-ABCD中,ABCD为矩形,平面PAD⊥平面ABCD.
如图,四棱锥P-ABCD中,ABCD为矩形,平面PAD⊥平面ABCD.(1)求证:AB⊥PD;
(2)若∠BPC=90°,PB=
| 2 |
考点:二面角的平面角及求法
专题:空间角,空间向量及应用
分析:(1)要证AD⊥PD,可以证明AB⊥面PAD,再利用面面垂直以及线面垂直的性质,即可证明AB⊥PD.
(2)过P做PO⊥AD得到PO⊥平面ABCD,作OM⊥BC,连接PM,由边长关系得到BC=
,PM=
,设AB=x,则VP-ABCD=
,故当x2=
时,VP-ABCD取最大值,建立空间直角坐标系O-AMP,利用向量方法即可得到夹角的余弦值.
(2)过P做PO⊥AD得到PO⊥平面ABCD,作OM⊥BC,连接PM,由边长关系得到BC=
| 6 |
| 2 | ||
|
| 1 |
| 3 |
| 8x2-6x4 |
| 2 |
| 3 |
解答:
 解:(1)∵在四棱锥P-ABCD中,ABCD为矩形,∴AB⊥AD,
解:(1)∵在四棱锥P-ABCD中,ABCD为矩形,∴AB⊥AD,
又∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
∴AB⊥面PAD,∴AB⊥PD.
(2)过P做PO⊥AD,∴PO⊥平面ABCD,
作OM⊥BC,连接PM
∴PM⊥BC,
∵∠BPC=90°,PB=
,PC=2,
∴BC=
,PM=
=
,BM=
,
设AB=x,∴OM=x∴PO=
,
∴VP-ABCD=
×x×
×
=
当x2=
,即x=
,VP-ABCD=
,
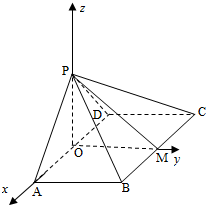
建立空间直角坐标系O-AMP,如图所示,
则P(0,0,
),D(-
,0,0),C(-
,
,0),M(0,
,0),B(
,
,0)
面PBC的法向量为
=(0,1,1),面DPC的法向量为
=(1,0,-2)
∴cosθ=|
|=|
|=
.
 解:(1)∵在四棱锥P-ABCD中,ABCD为矩形,∴AB⊥AD,
解:(1)∵在四棱锥P-ABCD中,ABCD为矩形,∴AB⊥AD,又∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
∴AB⊥面PAD,∴AB⊥PD.
(2)过P做PO⊥AD,∴PO⊥平面ABCD,
作OM⊥BC,连接PM
∴PM⊥BC,
∵∠BPC=90°,PB=
| 2 |
∴BC=
| 6 |
| 2 | ||
|
2
| ||
| 3 |
| ||
| 3 |
设AB=x,∴OM=x∴PO=
|
∴VP-ABCD=
| 1 |
| 3 |
| 6 |
|
| 1 |
| 3 |
| 8x2-6x4 |
当x2=
| 2 |
| 3 |
| ||
| 3 |
2
| ||
| 9 |
建立空间直角坐标系O-AMP,如图所示,
则P(0,0,
| ||
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
面PBC的法向量为
| n |
| m |
∴cosθ=|
| ||||
|
|
| -2 | ||||
|
| ||
| 5 |
点评:本题考查线面位置关系、线线位置关系、线面角的度量,考查分析解决问题、空间想象、转化、计算的能力与方程思想.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
设一组数据31,37,33,a,35的平均数是34,则这组数据的方差是( )
| A、2.5 | B、3 | C、3.5 | D、4 |
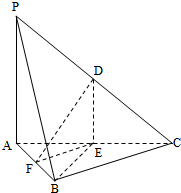 如图,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点,已知PA⊥AC,PA=6,BC=8,DF=5.求证:
如图,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点,已知PA⊥AC,PA=6,BC=8,DF=5.求证: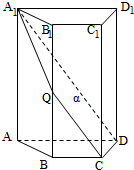 如图,四棱柱ABCD-A1B1C1D1中,A1A⊥底面ABCD,四边形ABCD为梯形,AD∥BC,且AD=2BC,过A1、C、D三点的平面记为α,BB1与α的交点为Q.
如图,四棱柱ABCD-A1B1C1D1中,A1A⊥底面ABCD,四边形ABCD为梯形,AD∥BC,且AD=2BC,过A1、C、D三点的平面记为α,BB1与α的交点为Q.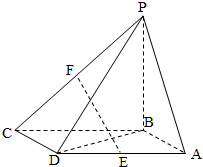 如图,四棱锥P-ABCD的底面ABCD是平行四边形,BA=BD=
如图,四棱锥P-ABCD的底面ABCD是平行四边形,BA=BD=