题目内容
甲、乙两名运动员各自等可能地从红、白、蓝3种颜色的运动服中选择1种,则他们选择相同颜色运动服的概率为 .
考点:相互独立事件的概率乘法公式
专题:概率与统计
分析:所有的选法共有3×3=9种,而他们选择相同颜色运动服的选法共有3种,由此求得他们选择相同颜色运动服的概率.
解答:
解:所有的选法共有3×3=9种,而他们选择相同颜色运动服的选法共有3种,
故他们选择相同颜色运动服的概率为
=
,
故答案为:
.
故他们选择相同颜色运动服的概率为
| 3 |
| 9 |
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:本题主要考查相互独立事件的概率乘法公式,属于基础题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
已知α、β、γ是三个不重合的平面,m、n是两条不重合的直线,下列命题为真命题的是( )
| A、m∥α,n∥α,则m∥n |
| B、α∥γ,n∥β,α∩β=m,则m∥n |
| C、α∥β,m?α,n?β,则m∥n |
| D、α∥γ,n?β,n?γ,α∩β=m,则m∥n |
设F是双曲线
-
=1的焦点,过F作双曲线一条渐近线的垂线,与两条渐近线交于P,Q,若
=3
,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| FP |
| FQ |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
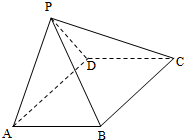 如图,四棱锥P-ABCD中,ABCD为矩形,平面PAD⊥平面ABCD.
如图,四棱锥P-ABCD中,ABCD为矩形,平面PAD⊥平面ABCD.