题目内容
已知F1，F2是双曲线
-
=1（a＞0，b＞0）的下、上焦点，点F2关于渐近线的对称点恰好落在以F1为圆心，|OF1|为半径的圆上，则双曲线的离心率为（ ）
| y2 |
| a2 |
| x2 |
| b2 |
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |
考点：双曲线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：首先求出F2到渐近线的距离，利用F2关于渐近线的对称点恰落在以F1为圆心，|OF1|为半径的圆上，可得直角三角形，即可求出双曲线的离心率．
解答：
解：由题意，F1（0，-c），F2（0，c），一条渐近线方程为y=
x，则F2到渐近线的距离为
=b．
设F2关于渐近线的对称点为M，F2M与渐近线交于A，∴|MF2|=2b，A为F2M的中点，
又0是F1F2的中点，∴OA∥F1M，∴∠F1MF2为直角，
∴△MF1F2为直角三角形，
∴由勾股定理得4c2=c2+4b2
∴3c2=4（c2-a2），∴c2=4a2，
∴c=2a，∴e=2．
故选：B．
| a |
| b |
| bc | ||
|
设F2关于渐近线的对称点为M，F2M与渐近线交于A，∴|MF2|=2b，A为F2M的中点，
又0是F1F2的中点，∴OA∥F1M，∴∠F1MF2为直角，
∴△MF1F2为直角三角形，
∴由勾股定理得4c2=c2+4b2
∴3c2=4（c2-a2），∴c2=4a2，
∴c=2a，∴e=2．
故选：B．
点评：本题主要考查了双曲线的几何性质以及有关离心率和渐近线，考查勾股定理的运用，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
已知弹簧的一端固定在地面上，另一端固定一个小球，已知小球在达到平衡位置之前处于加速状态，且加速度与时间的函数关系为a（t）=2t+
+3，则当t=1时小球的速度为（ ）
| 10 |
| 1+t |
| A、4+10ln2 |
| B、5+10ln2 |
| C、4-10ln2 |
| D、5-10ln2 |
已知双曲线
-
=1（a＞0，b＞0），A1、A2是双曲线的顶点，F是右焦点，点B（0，b），若在线段BF上（不含端点）存在不同的两点Pi（i=1，2），使得△PiA1A2（i=1，2）构成以线段A1A2为斜边的直角三角形，则双曲线离心率e的取值范围是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、（
| ||||||
B、（
| ||||||
C、（1，
| ||||||
D、（
|
复数z=i（i+1），在复平面内，与复数z对应的点Z所在的象限是（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知集合A={-2，-1，1，2}，B={x|x2-x-2≥0}，则A∩（∁RB）=（ ）
| A、{1} |
| B、{-1，1} |
| C、{-2，1，2} |
| D、{-2，-1，1} |
设△ABC的内角A、B、C所对的边a、b、c成等比数列，且公比为q，则q+
的取值范围是（ ）
| sinB |
| sinA |
| A、（0，+∞） | ||||
B、（0，
| ||||
C、（
| ||||
D、（
|
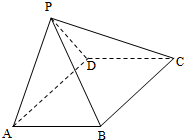如图，四棱锥P-ABCD中，ABCD为矩形，平面PAD⊥平面ABCD．