题目内容
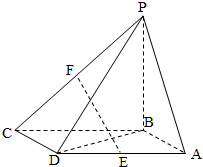 如图,四棱锥P-ABCD的底面ABCD是平行四边形,BA=BD=
如图,四棱锥P-ABCD的底面ABCD是平行四边形,BA=BD=| 2 |
| 5 |
(Ⅰ)证明EF∥平面PAB;
(Ⅱ)若二面角P-AD-B为60°,
(i)证明平面PBC⊥平面ABCD;
(ii)求直线EF与平面PBC所成角的正弦值.
考点:二面角的平面角及求法,直线与平面平行的判定,平面与平面垂直的判定,直线与平面所成的角
专题:空间角,空间向量及应用,立体几何
分析:(Ⅰ)要证明EF∥平面PAB,可以先证明平面EFH∥平面PAB,而要证明面面平行则可用面面平行的判定定理来证;
(Ⅱ)(i)要证明平面PBC⊥平面ABCD,可用面面垂直的判定定理,即只需证PB⊥平面ABCD即可;
(ii)由(i)知,BD,BA,BP两两垂直,建立空间直角坐标系B-DAP,得到直线EF的方向向量与平面PBC法向量,其夹角的余弦值的绝对值即为所成角的正弦值.
(Ⅱ)(i)要证明平面PBC⊥平面ABCD,可用面面垂直的判定定理,即只需证PB⊥平面ABCD即可;
(ii)由(i)知,BD,BA,BP两两垂直,建立空间直角坐标系B-DAP,得到直线EF的方向向量与平面PBC法向量,其夹角的余弦值的绝对值即为所成角的正弦值.
解答:
解:(Ⅰ)证明:连结AC,AC∩BD=H,
∵底面ABCD是平行四边形,∴H为BD中点,
∵E是棱AD的中点.∴在△ABD中,EH∥AB,
又∵AB?平面PAB,EH?平面PAD,∴EH∥平面PAB.
同理可证,FH∥平面PAB.
又∵EH∩FH=H,∴平面EFH∥平面PAB,
∵EF?平面EFH,∴EF∥平面PAB;

(Ⅱ)(i)如图,连结PE,BE.
∵BA=BD=
,AD=2,PA=PD=
,∴BE=1,PE=2.
又∵E为AD的中点,∴BE⊥AD,PE⊥AD,
∴∠PEB即为二面角P-AD-B的平面角,即∠PEB=60°,∴PB=
.
∵△PBD中,BD2+PB2=PD2,∴PB⊥BD,同理PB⊥BA,
∴PB⊥平面ABD,
∵PB?平面PBC,∴平面PAB⊥平面ABCD;
(ii)由(i)知,PB⊥BD,PB⊥BA,
∵BA=BD=
,AD=2,∴BD⊥BA,
∴BD,BA,BP两两垂直,
以B为坐标原点,分别以BD,BA,BP为X,Y,Z轴,建立如图所示的空间直角坐标系B-DAP,
则有A(0,
,0),B(0,0,0),C(
,-
,0),D(
,0,0),P(0,0,
),
∴
=(
,-
,0),
=(0,0,
),
设平面PBC的法向量为
=(x,y,z),
∵
,∴
,令x=1,则y=1,z=0,
故
=(1,1,0),
∵E,F分别是棱AD,PC的中点,
∴E(
,
,0),F(
,-
,
),
∴
=(0,-
,
),
∴cos<
,
>=
=
=-
,
即直线EF与平面PBC所成角的正弦值为
.
∵底面ABCD是平行四边形,∴H为BD中点,
∵E是棱AD的中点.∴在△ABD中,EH∥AB,
又∵AB?平面PAB,EH?平面PAD,∴EH∥平面PAB.
同理可证,FH∥平面PAB.
又∵EH∩FH=H,∴平面EFH∥平面PAB,
∵EF?平面EFH,∴EF∥平面PAB;

(Ⅱ)(i)如图,连结PE,BE.
∵BA=BD=
| 2 |
| 5 |
又∵E为AD的中点,∴BE⊥AD,PE⊥AD,
∴∠PEB即为二面角P-AD-B的平面角,即∠PEB=60°,∴PB=
| 3 |
∵△PBD中,BD2+PB2=PD2,∴PB⊥BD,同理PB⊥BA,
∴PB⊥平面ABD,
∵PB?平面PBC,∴平面PAB⊥平面ABCD;
(ii)由(i)知,PB⊥BD,PB⊥BA,
∵BA=BD=
| 2 |
∴BD,BA,BP两两垂直,
以B为坐标原点,分别以BD,BA,BP为X,Y,Z轴,建立如图所示的空间直角坐标系B-DAP,
则有A(0,
| 2 |
| 2 |
| 2 |
| 2 |
| 3 |
∴
| BC |
| 2 |
| 2 |
| BP |
| 3 |
设平面PBC的法向量为
| n |
∵
|
|
故
| n |
∵E,F分别是棱AD,PC的中点,
∴E(
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
∴
| EF |
| 2 |
| ||
| 2 |
∴cos<
| n |
| EF |
| ||||
|
|
-
| ||||||
|
2
| ||
| 11 |
即直线EF与平面PBC所成角的正弦值为
2
| ||
| 11 |
点评:本题主要考查空间直线与平面平行的判定定理以及线面角大小的求法,要求熟练掌握相关的判定定理.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
复数z=i(i+1),在复平面内,与复数z对应的点Z所在的象限是( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
设F是双曲线
-
=1的焦点,过F作双曲线一条渐近线的垂线,与两条渐近线交于P,Q,若
=3
,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| FP |
| FQ |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
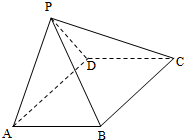 如图,四棱锥P-ABCD中,ABCD为矩形,平面PAD⊥平面ABCD.
如图,四棱锥P-ABCD中,ABCD为矩形,平面PAD⊥平面ABCD.