题目内容
设一组数据31，37，33，a，35的平均数是34，则这组数据的方差是（ ）
| A、2.5 | B、3 | C、3.5 | D、4 |
考点：极差、方差与标准差
专题：概率与统计
分析：先由数据的平均数公式求得x，再根据方差的公式计算．
解答：
解：这组数据31，37，33，a，35的平均数是34，则有34=
(31+37+33+a+35)
解得a=34
∴方差S2=
(9+9+1+0+1)=4
故选：D．
| 1 |
| 5 |
解得a=34
∴方差S2=
| 1 |
| 5 |
故选：D．
点评：本题考查一组数据的平均数、方差公式，属于基础题．
练习册系列答案
综合自测系列答案
相关题目
已知弹簧的一端固定在地面上，另一端固定一个小球，已知小球在达到平衡位置之前处于加速状态，且加速度与时间的函数关系为a（t）=2t+
+3，则当t=1时小球的速度为（ ）
| 10 |
| 1+t |
| A、4+10ln2 |
| B、5+10ln2 |
| C、4-10ln2 |
| D、5-10ln2 |
已知复数z=（x2-1）+（x+1）i（x∈R，i是虚数单位）是纯虚数，则x的值为（ ）
| A、-1 | B、1 | C、±1 | D、0 |
设m∈R，则m=1是直线l1：（m+1）x+2y-1=0和l2：x+my+4=0平行的（ ）
| A、充分必要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分又不必要条件 |
已知双曲线
-
=1（a＞0，b＞0），A1、A2是双曲线的顶点，F是右焦点，点B（0，b），若在线段BF上（不含端点）存在不同的两点Pi（i=1，2），使得△PiA1A2（i=1，2）构成以线段A1A2为斜边的直角三角形，则双曲线离心率e的取值范围是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、（
| ||||||
B、（
| ||||||
C、（1，
| ||||||
D、（
|
复数z=i（i+1），在复平面内，与复数z对应的点Z所在的象限是（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
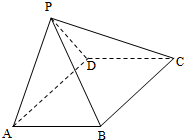如图，四棱锥P-ABCD中，ABCD为矩形，平面PAD⊥平面ABCD．