题目内容
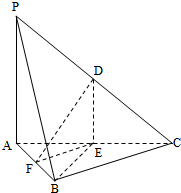 如图,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点,已知PA⊥AC,PA=6,BC=8,DF=5.求证:
如图,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点,已知PA⊥AC,PA=6,BC=8,DF=5.求证:(1)直线PA∥平面DEF;
(2)平面BDE⊥平面ABC.
考点:平面与平面垂直的判定,直线与平面垂直的判定
专题:空间位置关系与距离,空间角,立体几何
分析:(1)由D、E为PC、AC的中点,得出DE∥PA,从而得出PA∥平面DEF;
(2)要证平面BDE⊥平面ABC,只需证DE⊥平面ABC,即证DE⊥EF,且DE⊥AC即可.
(2)要证平面BDE⊥平面ABC,只需证DE⊥平面ABC,即证DE⊥EF,且DE⊥AC即可.
解答:
证明:(1)∵D、E为PC、AC的中点,∴DE∥PA,
又∵PA?平面DEF,DE?平面DEF,
∴PA∥平面DEF;
(2)∵D、E为PC、AC的中点,∴DE=
PA=3;
又∵E、F为AC、AB的中点,∴EF=
BC=4;
∴DE2+EF2=DF2,
∴∠DEF=90°,
∴DE⊥EF;
∵DE∥PA,PA⊥AC,∴DE⊥AC;
∵AC∩EF=E,∴DE⊥平面ABC;
∵DE?平面BDE,∴平面BDE⊥平面ABC.
又∵PA?平面DEF,DE?平面DEF,
∴PA∥平面DEF;
(2)∵D、E为PC、AC的中点,∴DE=
| 1 |
| 2 |
又∵E、F为AC、AB的中点,∴EF=
| 1 |
| 2 |
∴DE2+EF2=DF2,
∴∠DEF=90°,
∴DE⊥EF;
∵DE∥PA,PA⊥AC,∴DE⊥AC;
∵AC∩EF=E,∴DE⊥平面ABC;
∵DE?平面BDE,∴平面BDE⊥平面ABC.
点评:本题考查了空间中的平行与垂直问题,解题时应明确空间中的线线、线面、面面之间的垂直与平行的互相转化关系,是基础题目.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
已知复数z=(x2-1)+(x+1)i(x∈R,i是虚数单位)是纯虚数,则x的值为( )
| A、-1 | B、1 | C、±1 | D、0 |
复数z=i(i+1),在复平面内,与复数z对应的点Z所在的象限是( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知集合A={-2,-1,1,2},B={x|x2-x-2≥0},则A∩(∁RB)=( )
| A、{1} |
| B、{-1,1} |
| C、{-2,1,2} |
| D、{-2,-1,1} |
设△ABC的内角A、B、C所对的边a、b、c成等比数列,且公比为q,则q+
的取值范围是( )
| sinB |
| sinA |
| A、(0,+∞) | ||||
B、(0,
| ||||
C、(
| ||||
D、(
|
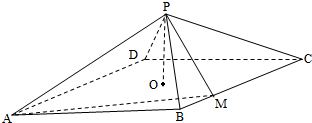 如图,四棱锥P-ABCD,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=
如图,四棱锥P-ABCD,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=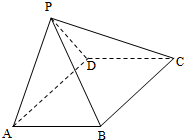 如图,四棱锥P-ABCD中,ABCD为矩形,平面PAD⊥平面ABCD.
如图,四棱锥P-ABCD中,ABCD为矩形,平面PAD⊥平面ABCD.