题目内容
设函数f(x)=lnx+
,m∈R.
(Ⅰ)当m=e(e为自然对数的底数)时,求f(x)的极小值;
(Ⅱ)讨论函数g(x)=f′(x)-
零点的个数;
(Ⅲ)若对任意b>a>0,
<1恒成立,求m的取值范围.
| m |
| x |
(Ⅰ)当m=e(e为自然对数的底数)时,求f(x)的极小值;
(Ⅱ)讨论函数g(x)=f′(x)-
| x |
| 3 |
(Ⅲ)若对任意b>a>0,
| f(b)-f(a) |
| b-a |
考点:利用导数研究函数的极值,函数恒成立问题,函数的零点
专题:导数的综合应用
分析:(Ⅰ)m=e时,f(x)=lnx+
,利用f′(x)判定f(x)的增减性并求出f(x)的极小值;
(Ⅱ)由函数g(x)=f′(x)-
,令g(x)=0,求出m;设φ(x)=m,求出φ(x)的值域,讨论m的取值,对应g(x)的零点情况;
(Ⅲ)由b>a>0,
<1恒成立,等价于f(b)-b<f(a)-a恒成立;即h(x)=f(x)-x在(0,+∞)上单调递减;h′(x)≤0,求出m的取值范围.
| e |
| x |
(Ⅱ)由函数g(x)=f′(x)-
| x |
| 3 |
(Ⅲ)由b>a>0,
| f(b)-f(a) |
| b-a |
解答:
 解:(Ⅰ)当m=e时,f(x)=lnx+
解:(Ⅰ)当m=e时,f(x)=lnx+
,
∴f′(x)=
;
∴当x∈(0,e)时,f′(x)<0,f(x)在(0,e)上是减函数;
当x∈(e,+∞)时,f′(x)>0,f(x)在(e,+∞)上是增函数;
∴x=e时,f(x)取得极小值f(e)=lne+
=2;
(Ⅱ)∵函数g(x)=f′(x)-
=
-
-
(x>0),
令g(x)=0,得m=-
x3+x(x>0);
设φ(x)=-
x3+x(x≥0),
∴φ′(x)=-x2+1=-(x-1)(x+1);
当x∈(0,1)时,φ′(x)>0,φ(x)在(0,1)上是增函数,
当x∈(1,+∞)时,φ′(x)<0,φ(x)在(1,+∞)上是减函数;
∴x=1是φ(x)的极值点,且是极大值点,
∴x=1是φ(x)的最大值点,
∴φ(x)的最大值为φ(1)=
;
又φ(0)=0,结合y=φ(x)的图象,如图;
可知:
①当m>
时,函数g(x)无零点;
②当m=
时,函数g(x)有且只有一个零点;
③当0<m<
时,函数g(x)有两个零点;
④当m≤0时,函数g(x)有且只有一个零点;
综上,当m>
时,函数g(x)无零点;
当m=
或m≤0时,函数g(x)有且只有一个零点;
当0<m<
时,函数g(x)有两个零点;
(Ⅲ)对任意b>a>0,
<1恒成立,
等价于f(b)-b<f(a)-a恒成立;
设h(x)=f(x)-x=lnx+
-x(x>0),
∴h(x)在(0,+∞)上单调递减;
∵h′(x)=
-
-1≤0在(0,+∞)上恒成立,
∴m≥-x2+x=-(x-
)2+
(x>0),
∴m≥
;
对于m=
,h′(x)=0仅在x=
时成立;
∴m的取值范围是[
,+∞).
 解:(Ⅰ)当m=e时,f(x)=lnx+
解:(Ⅰ)当m=e时,f(x)=lnx+| e |
| x |
∴f′(x)=
| x-e |
| x2 |
∴当x∈(0,e)时,f′(x)<0,f(x)在(0,e)上是减函数;
当x∈(e,+∞)时,f′(x)>0,f(x)在(e,+∞)上是增函数;
∴x=e时,f(x)取得极小值f(e)=lne+
| e |
| e |
(Ⅱ)∵函数g(x)=f′(x)-
| x |
| 3 |
| 1 |
| x |
| m |
| x2 |
| x |
| 3 |
令g(x)=0,得m=-
| 1 |
| 3 |
设φ(x)=-
| 1 |
| 3 |
∴φ′(x)=-x2+1=-(x-1)(x+1);
当x∈(0,1)时,φ′(x)>0,φ(x)在(0,1)上是增函数,
当x∈(1,+∞)时,φ′(x)<0,φ(x)在(1,+∞)上是减函数;
∴x=1是φ(x)的极值点,且是极大值点,
∴x=1是φ(x)的最大值点,
∴φ(x)的最大值为φ(1)=
| 2 |
| 3 |
又φ(0)=0,结合y=φ(x)的图象,如图;
可知:
①当m>
| 2 |
| 3 |
②当m=
| 2 |
| 3 |
③当0<m<
| 2 |
| 3 |
④当m≤0时,函数g(x)有且只有一个零点;
综上,当m>
| 2 |
| 3 |
当m=
| 2 |
| 3 |
当0<m<
| 2 |
| 3 |
(Ⅲ)对任意b>a>0,
| f(b)-f(a) |
| b-a |
等价于f(b)-b<f(a)-a恒成立;
设h(x)=f(x)-x=lnx+
| m |
| x |
∴h(x)在(0,+∞)上单调递减;
∵h′(x)=
| 1 |
| x |
| m |
| x2 |
∴m≥-x2+x=-(x-
| 1 |
| 2 |
| 1 |
| 4 |
∴m≥
| 1 |
| 4 |
对于m=
| 1 |
| 4 |
| 1 |
| 2 |
∴m的取值范围是[
| 1 |
| 4 |
点评:本题考查了导数的综合应用问题,解题时应根据函数的导数判定函数的增减性以及求函数的极值和最值,应用分类讨论法,构造函数等方法来解答问题,是难题.

练习册系列答案
相关题目
已知集合A={-2,-1,1,2},B={x|x2-x-2≥0},则A∩(∁RB)=( )
| A、{1} |
| B、{-1,1} |
| C、{-2,1,2} |
| D、{-2,-1,1} |
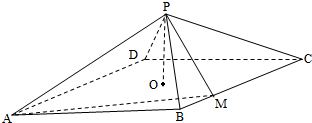 如图,四棱锥P-ABCD,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=
如图,四棱锥P-ABCD,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=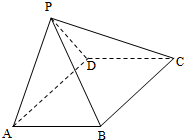 如图,四棱锥P-ABCD中,ABCD为矩形,平面PAD⊥平面ABCD.
如图,四棱锥P-ABCD中,ABCD为矩形,平面PAD⊥平面ABCD.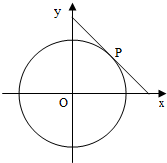 圆x2+y2=4的切线与x轴正半轴,y轴正半轴围成一个三角形,当该三角形面积最小时,切点为P(如图).
圆x2+y2=4的切线与x轴正半轴,y轴正半轴围成一个三角形,当该三角形面积最小时,切点为P(如图).