题目内容
f(x)满足f(x+2)=-f(x),当0≤x≤1时,f(x)=x,f(x)是奇函数,则F(x)=f(x)-lgx的零点有 个.
考点:根的存在性及根的个数判断
专题:计算题,函数的性质及应用
分析:由题意,F(x)=f(x)-lgx的零点个数即函数f(x)与lgx的交点个数,作出函数f(x)与lgx的图象,找到交点个数即可.
解答:
解:F(x)=f(x)-lgx的零点个数即函数f(x)与lgx的交点个数,
由f(x)满足f(x+2)=-f(x),当0≤x≤1时,f(x)=x,f(x)是奇函数,
作出函数f(x)与lgx的图象如下:

由图可知,有5个交点,
故答案为:5.
由f(x)满足f(x+2)=-f(x),当0≤x≤1时,f(x)=x,f(x)是奇函数,
作出函数f(x)与lgx的图象如下:

由图可知,有5个交点,
故答案为:5.
点评:本题考查了学生的作图能力及函数的零点与函数的图象的关系,属于基础题.

练习册系列答案
相关题目

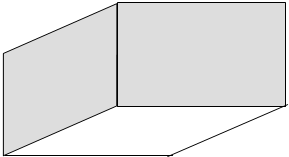 如图,用一块长为2米,宽为1米的矩形木板,在教室的墙角处围出一个直三棱柱的储物角(使木板垂直于地面的两边与墙面贴紧),试问应怎样围才能使储物角的容积最大?并求出这个最大值.
如图,用一块长为2米,宽为1米的矩形木板,在教室的墙角处围出一个直三棱柱的储物角(使木板垂直于地面的两边与墙面贴紧),试问应怎样围才能使储物角的容积最大?并求出这个最大值.