题目内容
若椭圆
+
=1的一个焦点坐标为（2，0），则m= ．
| x2 |
| m |
| y2 |
| 4 |
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：利用椭圆
+
=1的一个焦点为（2，0），可得m-4=4，即可求出m的值．
| x2 |
| m |
| y2 |
| 4 |
解答：
解：∵椭圆
+
=1的一个焦点为（2，0），焦点在x轴上，
∴m-4=4，
∴m=8．
故答案为：8．
| x2 |
| m |
| y2 |
| 4 |
∴m-4=4，
∴m=8．
故答案为：8．
点评：本题考查椭圆的标准方程的应用，是基础题，解题时要认真审题，注意椭圆简单性质的灵活运用．
练习册系列答案
相关题目
若f：A→B能构成映射，下列说法正确的有（ ）
（1）A中的任一元素在B中必须有像且唯一；
（2）A中的多个元素可以在B中有相同的像；
（3）B中的多个元素可以在A中有相同的原像；
（4）B中的任一元素在A中必须有像．
（1）A中的任一元素在B中必须有像且唯一；
（2）A中的多个元素可以在B中有相同的像；
（3）B中的多个元素可以在A中有相同的原像；
（4）B中的任一元素在A中必须有像．
| A、1个 | B、2个 | C、3个 | D、0个 |
已知全集U=R，集合A={x|a≤x≤b}，集合B={x|x2-x-2＞0}，若A∩B=φ，A∪B=U，则a，b的值分别是（ ）
| A、-1，2 | B、2，-1 |
| C、-1，1 | D、-2，2 |
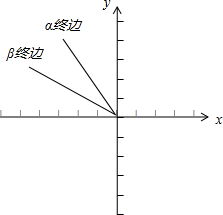已知α是第二象限角，在第二象限内将角α的终边绕原点按逆时针方向旋转，得到第二象限角β的终边，如图所示，利用单位圆中的三角函数线比较下列各组数的大小．